Abstract
가중치를 크기와 방향이라는 2가지 구성요소로 분해하여 효율적이고 정확하게 fine-tuning 할 수 있는 DoRA 제안
[Github]
[arXiv](2024/03/05 version v3)
Pattern Analysis of LoRA and FT
Low-Rank Adaptation (LoRA)

Weight Decomposition Analysis
가중치를 크기 벡터 m, 방향 행렬 V로 분해하여 LoRA와 Fine-tuning (모든 가중치)의 근본적인 차이를 밝힌다.

VL-BART의 Q, V 가중치 행렬의 original weight, fine-tuned weight, merged LoRA weight를 분해하여 크기, 방향의 변화를 다음과 같이 측정한다.


LoRA는 크기와 방향의 변화가 비례하는 특정 패턴을 가진다.
본문에서 제안하는 DoRA의 경우 FT와 유사한 추세를 가지는 것을 볼 수 있다.
Method
Weight-Decomposed Low-Rank Adaptation
DoRA는 가중치를 크기와 방향으로 분해한 뒤 방향 행렬을 다시 low-rank로 분해한다.

원본 행렬인 V는 고정되고 m, A, B만 훈련한다.

Reduction of Training Overhead
m과 V ′ = V + ∆V의 gradient는 다음과 같다.
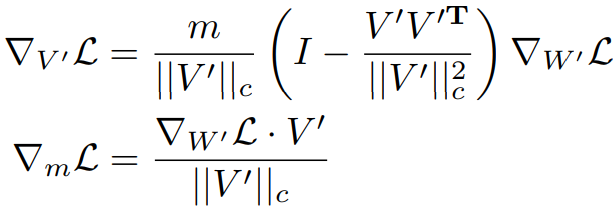
LoRA에서는 W '와 ∆W의 gradient가 같지만 DoRA에서는 m, V '가 W '를 구성하므로 gradient에 대한 추가 처리가 필요하며 이는 훈련 오버헤드의 증가로 이어진다.
V '의 크기를 상수로 취급하여 gradient graph에서 분리하면 큰 성능차이 없이 메모리를 크게 줄일 수 있다.
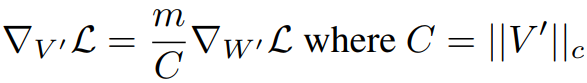

Experiments

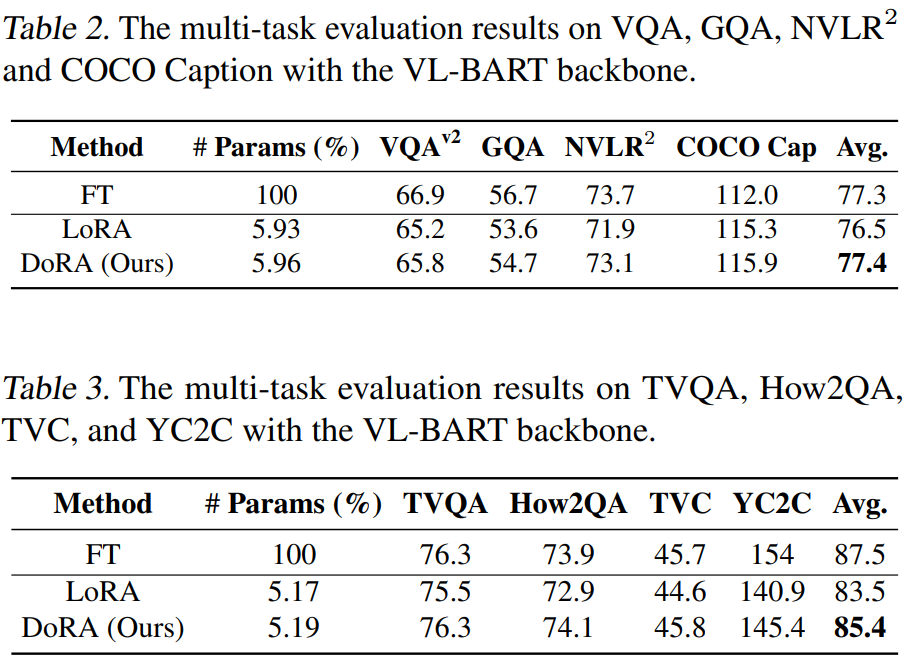
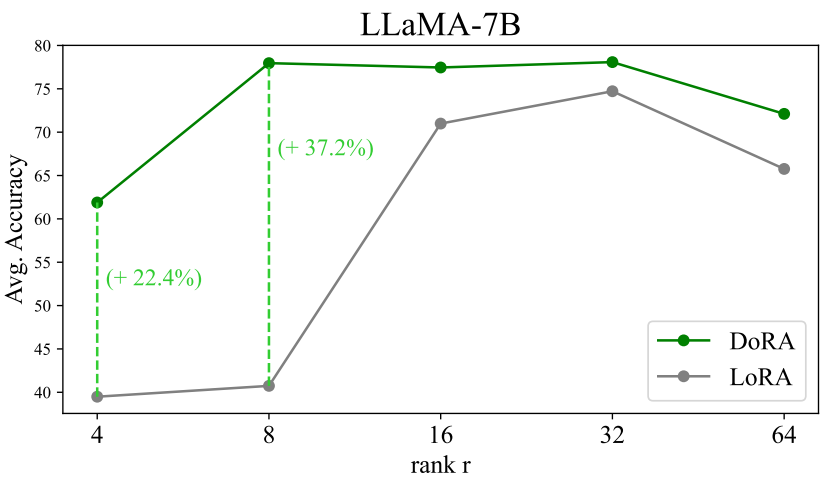
Low-Rank에서 더 견고하다.
'논문 리뷰 > Language Model' 카테고리의 다른 글
| Mini-Gemini: Mining the Potential of Multi-modality Vision Language Models (0) | 2024.04.01 |
|---|---|
| Quiet-STaR: Language Models Can Teach Themselves to Think Before Speaking (0) | 2024.03.27 |
| STaR: Bootstrapping Reasoning With Reasoning (0) | 2024.03.27 |
| LoRA+: Efficient Low Rank Adaptation of Large Models (0) | 2024.03.22 |
| RAFT: Adapting Language Model to Domain Specific RAG (0) | 2024.03.21 |
| MoAI: Mixture of All Intelligence for Large Language and Vision Models (0) | 2024.03.19 |



