

Abstract
LoRA의 A, B 행렬에 각각 다른 학습률을 적용하여 더 효율적으로 훈련
[Github]
[arXiv](2024/02/19 version v1)
An Intuitive Analysis of LoRA
Low-Rank Adaptation (LoRA)
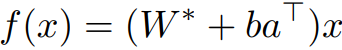
Initialization
일반적으로 a, b 중 하나를 0으로 초기화하며 b를 0으로 초기화할 경우 a는 많이 쓰이는 초기화 방식에 따라 입력 활성화의 크기 n에 반비례하는 분산을 가진다. 이는 큰 활성화의 생성을 방지해 학습을 안정화시킨다.

y = Θ(x)는 y가 x에 대한 linear scale을 가진다는 것을 의미한다. y = k*x
Learning rate
분석의 단순화를 위해 W* = 0으로 가정하면 gradients는 다음과 같이 작성할 수 있다.

b는 ax와 loss에 영향을 받고 a는 b, x와 loss에 영향을 받는다.
한 차례 학습이 진행된 후 입력 x에 대한 출력 f(x)의 변화율은 다음과 같다.
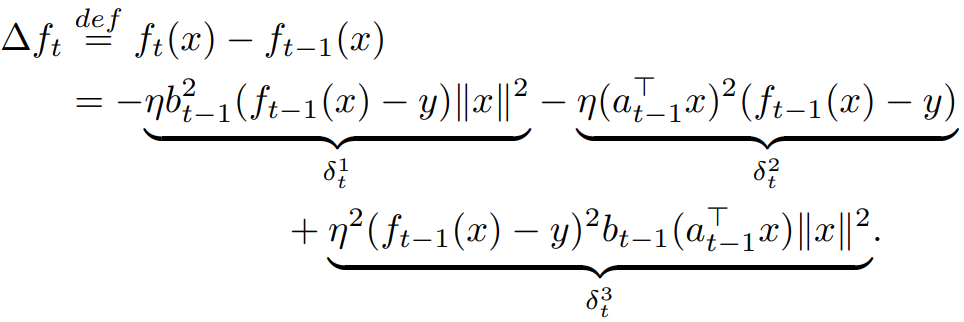
순서대로 a의 업데이트에 의한 변화, b의 업데이트에 의한 변화, a&b의 업데이트에 의한 변화
우리의 목표는 n의 크기에 상관없이, 특히 n → ∞일 때 안정된 학습을 가능하게 하는 학습률 η를 찾는 것이다.
(최근 LLM 모델들의 너비가 매우 커지는 상황이므로)
즉, δ1, 2, 3 = Θ(1)을 만족하게 하는 특정 η를 찾아야 한다.
δ1 = Θ(1)을 만족하려면 η = Θ(n-1) 이어야 하는데, 그러면 δ2 = Θ(n-1)이 되고
δ2 = Θ(1)을 만족하려면 η = Θ(1) 이어야 하며, 그러면 δ1 = Θ(n)이 된다.
쉽게 설명하자면, 큰 n에서 a의 불안정한 학습을 막기 위해 학습률을 낮추면 b의 학습이 비효율적이게 된다.
한 가지 쉬운 해결책은 a와 b에 다른 학습률을 적용하고 a의 학습률만 낮추는 것이다.
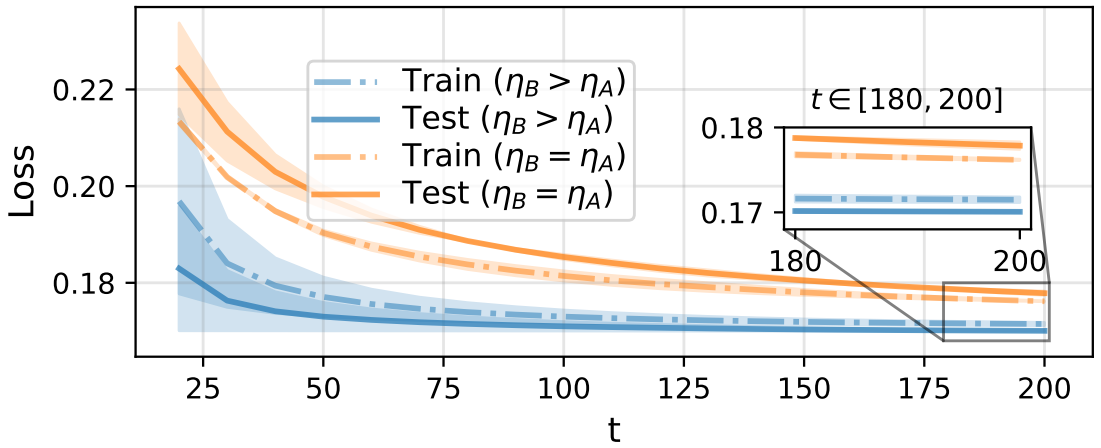
Abstract의 언급에 따르면 최대 2배까지 더 빠르게 학습 가능하며 1~2%의 성능 향상이 있다고 하긴 하는데 그 정도면 의미는 없는 거 같고 아무튼 빠르긴 하다.

'논문 리뷰 > Language Model' 카테고리의 다른 글
| Quiet-STaR: Language Models Can Teach Themselves to Think Before Speaking (0) | 2024.03.27 |
|---|---|
| STaR: Bootstrapping Reasoning With Reasoning (0) | 2024.03.27 |
| DoRA: Weight-Decomposed Low-Rank Adaptation (0) | 2024.03.26 |
| RAFT: Adapting Language Model to Domain Specific RAG (0) | 2024.03.21 |
| MoAI: Mixture of All Intelligence for Large Language and Vision Models (0) | 2024.03.19 |
| Chronos: Learning the Language of Time Series (0) | 2024.03.19 |



