5월 5일 공개된 Neural 3D Scene Reconstruction with the Manhattan-world Assumption
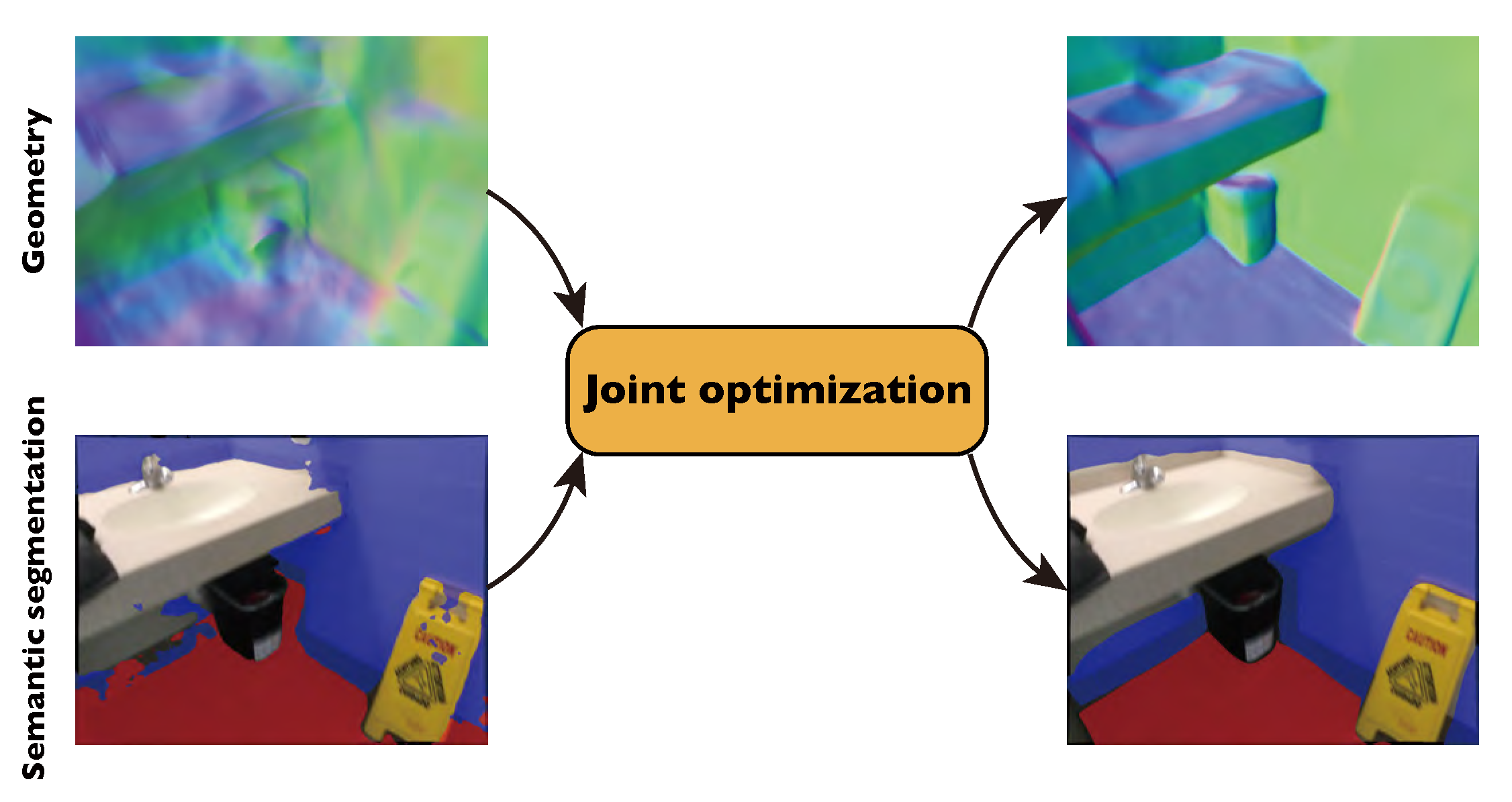

3D 복원 분야는 익숙하지 않아 요약할 수가 없어서 글이 좀 길 수 있습니다...
Abstract
이 논문은 멀티 뷰 이미지에서 3D 실내 장면(=Scene)을 재구성하는 문제를 다룬다. 이전의 많은 작품들은 질감(=texture)이 있는 물체에서 인상적인 재구성 결과를 보여주었지만, 여전히 실내 장면에서 흔히 볼 수 있는 질감이 낮은 평면 영역을 다루는 데 어려움을 겪고 있다. 이 문제를 해결하기 위한 접근법은 멀티뷰 스테레오 기반 방법의 깊이 맵 추정에 평면 제약 조건을 통합하는 것이지만, 뷰별 평면 추정과 깊이 최적화는 효율성과 멀티뷰 일관성이 모두 부족하다. 본 연구에서는 평면 제약 조건이 최근의 암묵적 신경 표현 기반 재구성 방법에 편리하게 통합될 수 있음을 보여준다. 특히, MLP 네트워크를 사용하여 Signed Distance Function(SDF)를 장면 geometry로 표현한다. Manhattan-world 가정에 기초하여, 평면 제약 조건은 2D semantic 분할 네트워크에 의해 예측된 바닥 및 벽 영역의 형상을 정규화하기 위해 사용된다. 부정확한 분할을 해결하기 위해 3D 점의 semantic을 다른 MLP로 인코딩하고 3D 공간에서 장면 geometry 및 semantic을 공동으로 최적화하는 새로운 손실을 설계한다.
Introduction
3D 장면 재구성에서 입력 이미지가 주어지면, 전통적인 방법은 일반적으로 multi-view stereo (MVS) 알고리즘을 기반으로 각 이미지에 대한 깊이 맵을 추정한 다음 추정된 깊이 맵을 3D 모델로 융합한다. 이러한 방법은 대부분의 경우 성공적인 재구성을 달성하지만, 신뢰할 수 없는 스테레오 매칭으로 인해 실내 장면의 바닥 및 벽과 같은 질감이 낮은 영역을 처리하는 데 어려움이 있다.
질감이 낮은 영역의 재구성을 개선하기 위해, 일반적인 접근법은 인공 장면보다 먼저 평면도를 활용하는 것인데, 유명한 예는 Manhattan-world 가정이다. 즉, 인공 장면의 표면은 세 가지 지배적인 방향으로 정렬되어야 한다. 이러한 작업은 표면 추정을 후처리 단계로 사용하여 저질감 영역에서 누락된 깊이 값을 색칠하거나 스테레오 매칭 또는 깊이 최적화에 평면 제약 조건을 통합한다. 그러나 이들 모두는 3D 공간에서 전체 장면 모델 대신 뷰별 깊이 맵을 최적화하는 데 중점을 둔다. 그 결과, 깊이 추정과 평면 분할은 여전히 뷰 간에 일관성이 없을 수 있다.
최근 3D 장면을 암시적 신경 표현으로 표현하고 미분 가능한 렌더러가 있는 이미지에서 표현을 배우는 경향이 있다. 특히 몇몇의 연구에서는 SDF를 사용하여 장면을 표현하고 구면 추적 또는 볼륨 렌더링을 기반으로 이미지를 렌더링한다. SDF의 잘 정의된 표면 덕분에 이미지에서 고품질 3D 형상을 복구할 수 있지만 이러한 방법은 기본적으로 SDF를 학습하기 위해 멀티 뷰의 광확적 일관성에 의존한다. 따라서 질감이 낮은 평면 영역에서는 여전히 성능이 저하된다.
이 연구에서, Manhattan-world 가정이 3D 실내 장면의 암시적 신경 표현 학습에 편리하게 통합될 수 있고 재구성 품질을 크게 향상시킬 수 있음을 보여준다. 뷰당 깊이 최적화를 수행하는 이전의 MVS 방법과 달리, 암시적 신경 표현은 3D 공간에서 장면 geometry 및 semantic의 공동 표현과 최적화를 동시에 가능하게 하여 일관된 재구성 및 분할을 산출한다. 특히, 본 연구에서는 MLP 네트워크를 사용하여 3D 공간의 모든 점에 대해 Signed Distance(SD), 색상 및 semantic logit을 예측한다. Semantic logit은 2D semantic 분할 네트워크에 의해 초기화된 점이 바닥, 벽 또는 배경이 될 확률을 나타낸다. NeuS, VolSDF와 유사하게, 볼륨 렌더링을 기반으로 렌더링된 이미지와 입력 이미지를 비교하여 SD와 색상 필드를 학습한다. 바닥과 벽에 있는 표면 점의 경우, Manhattan-world의 가정을 존중하기 위해 표면 법선(=normal)을 시행한다. 초기 분할이 정확하지 않을 수 있다는 점을 고려하여 SDF와 함께 semantic logit을 동시에 최적화하는 손실을 설계한다. 이 손실은 장면 재구성 및 semantic 분할을 효과적으로 개선한다.
본 연구의 기여는 다음과 같다.
- Manhattan-world 제약을 암시적 신경 표현의 최적화에 통합하는 새로운 장면 재구성 접근 방식
- 장면 geometry와 함께 semantic label을 최적화하는 새로운 손실 함수
- SOTA 방법과 비교하여 재구성 품질의 상당한 향상
Method
본 논문에서는 다음과 그림과 같이 Manhattan SDF 라는 새로운 접근법을 제안한다.
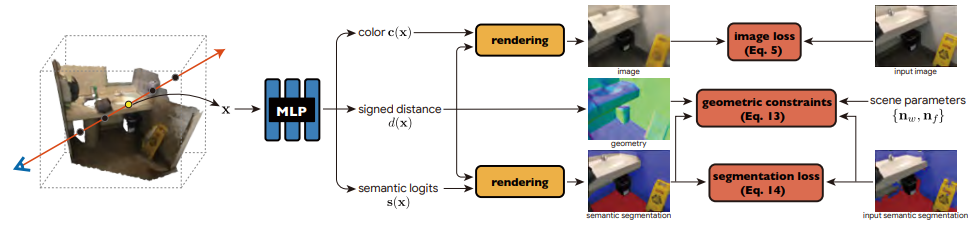
장면 geometry 및 외관을 SD 및 색상 필드로 나타내며, 이는 볼륨 렌더링 기술을 사용한 이미지에서 학습된다. 질감이 없는 영역에서 재구성 품질을 향상시키기 위해 semantic 분할을 수행하여 이러한 영역을 감지하고 Manhattan-world 가정에 기초한 기하학적 제약 조건을 적용한다. Semantic 분할의 부정확성을 극복하기 위해 semantic 정보를 암묵적인 장면 표현으로 추가로 인코딩하고 장면의 geometry 및 외관과 함께 semantic 정보를 공동으로 최적화한다.
Learning scene representations from images
장면을 암시적 신경 표현으로 모델링하고 미분 가능한 렌더러가 있는 이미지에서 학습한다. 그리고 SD 및 색상 필드로 장면 geometry 및 외관을 나타낸다.
구체적으로, 3D 점 x가 주어지면 geometry 모델은 다음과 같이 정의된 SD d(x)에 매핑한다.

F는 MLP로 구현되며, z는 Implicit Differentiable Renderer (IDR)에서의 geometry feature를 추출하는 학습가능한 피라미터이다.
빛 방사 함수를 근사하기 위해, 외관 모델은 점 x, 뷰 방향 v, 법선 n(x) 및 geometry feature z(x)를 입력 및 출력 색상 c(x)로 취한다.

법선 n(x)는 지점 x에서 SD d(x)의 기울기를 계산하여 구한다.
그리고 볼륨 렌더링을 채택하여 이미지에서 장면 표현 네트워크를 학습한다.

볼륨 렌더링은 하나의 카메라 광선(=ray)에서 여러 개의 점을 샘플링함으로써 갑작스러운 깊이 변화에도 유연하게 처리할 수 있다.
구체적으로, 이미지 픽셀을 렌더링하기 위해 카메라 광선 r을 따라 N개의 점 {xi}를 샘플링한 뒤 각 점의 SD와 색상을 예측한다. 볼륨 렌더링을 적용하기 위해 SD d(x)를 볼륨 밀도 σ(x)로 변환한 후,

β는 학습가능한 피라미터이다.
그런 다음 numerical quadrature를 이용하여 밀도와 색상을 누적한다.
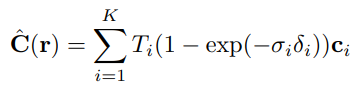
δ는 인접한 두 점 사이의 거리, T는 광선을 따라 누적된 투과율을 의미한다.
다음과 같은 photometric loss를 사용하여 장면 표현 네트워크를 최적화한다.

C는 색상의 ground truth, R은 카메라 광선들의 집합.
그리고 Eikonal loss를 사용한다.

Eikonal 방정식은 파동 전파 문제에서 발생하는 기하학적 광학의 고전적인 방정식이다.
이 식에 대해 참조 논문 빼고는 전혀 설명이 없어서 조금 읽어봤다.
임의의 점 구름의 점 집합 X와 임의의 법선 n에 대해


위의 식의 값이 최소가 되는 경우는 함수 f가 법선 n의 방향을 기준으로 하는 SDF 일 때 라고 한다.
그래서 결론적으로 eikonal loss는 d(x)의 피라미터를 최적화 하기 위해 사용하는 것이다.
연구진은 아래 그림의 (a)에서와 같이, 이미지만으로 장면 표현을 처음부터 학습하는 것은 질감이 있는 영역에서도 합리적인 기하학적 구조를 재구성하는 데 어려움이 있음을 관찰한다.

깊이 추정 기반 방법은 질감이 낮은 영역에서 불완전한 재구성을 제공하는 경향이 있지만, 이미지에서 질감이 있는 영역의 정확한 점 구름을 재구성할 수 있다. 연구진은 장면 표현의 학습을 돕기 위해 이 논문에서 제안된 멀티 뷰 스테레오 방법의 깊이 맵을 사용할 것을 제안한다.

D는 추정된 깊이 값을 갖는 이미지 픽셀을 통과하는 카메라 광선의 집합이다.
깊이 손실을 활용한 재구성은 위의 (b)에서 볼 수 있다. 질감이 없는 부분은 여전히 불완전하다.
Scene reconstruction with planar constraints
Manhattan-world 가정에서 지적된 바와 같이 바닥과 벽은 일반적으로 세 가지 방향축과 일치한다. 이에 자극 받아, 바닥과 벽의 영역에 기하학적 제약을 적용할 것을 제안한다.
먼저 바닥과 벽의 영역을 얻기 위해 2D semantic 분할 네트워크를 사용한다. 그런 다음 손실 함수를 적용하여 평면 영역의 표면 점들이 동일한 법선 방향을 공유하도록 한다.
바닥은 z축에 수직이라고 가정하며 손실을 다음과 같이 설계한다.
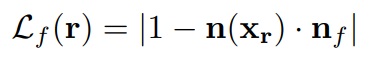
xr은 카메라 광선 r의 표면 교차점, n(xr)은 xr에서의 SD d(x)의 기울기로 계산된 법선, nf는 바닥의 법선 방향을 나타내는 단위벡터 <0,0,1>.
벽 영역의 감독을 위해 학습 가능한 법선 nw를 도입한다. 벽 표면 점의 법선 방향이 nw와 평행하거나 직교하도록 하는 손실을 설계한다.

nw는 <1,0,0>으로 초기화되어 훈련 중 최적화되며 마지막 원소는 0으로 고정한다.
최종적인 손실함수는

F, W는 semantic 분할에 의해 바닥 및 벽으로 예측되는 이미지 픽셀의 카메라 광선의 집합이다.
재구성 결과는 위 그림의 (c)에서 볼 수 있다.
Joint optimization of semantics and geometry
재구성 품질을 조금 더 개선하기 위해, 장면 geometry 및 외관과 함께 3D에서의 semantic label을 최적화할 것을 제안한다.
Semantic-NeRF에서 영감을 받아 3D 공간의 각 점에 대한 semantic logit을 추가로 예측하여 표현을 강화한다.
x에 대한 semantic logit을 s(x) ∈ R3라 하자. s(x)는 다음과 같이 나타낼 수 있다.

Fs는 MLP 네트워크이며 softmax를 적용하면 logit이 점 x가 바닥, 벽 또는 기타 물체일 확률로 변환될 수 있다.
볼륨 렌더링 기술을 사용하여 semantic logit들을 2D 이미지 공간으로 렌더링한다. 다음과 같이 나타낼 수 있다.

si는 카메라 광선을 따라 샘플링된 점 xi의 logit이다.
그리고 Ŝ를 softmax 정규화 계층으로 전달하여 바닥, 벽 또는 물체일 확률 p̂f, p̂w, p̂b를 계산한다.
이렇게 구한 클래스 확률을 바닥과 벽의 geometry 손실과 통합한다.

클래스 예측이 잘못되었을 때 훈련에 지장이 생기는 것을 방지하기 위해 여기에 교차 엔트로피 손실을 추가하여 추가적인 감독을 한다.

p̂k는 클래스 k가 렌더링된 확률, pk는 2D semantic 예측이다.
Ls로 3D semantic을 학습하면 Semantic-NeRF에서와 같이 멀티뷰 의견 합치를 자연스럽게 활용하여 semantic 장면 분할의 정확도를 향상할 수 있다.
(모든 손실함수를 종합하는 부분은 없고 여기서 끝나네요.)
Implementation details
Semantic 분할 네트워크로 Detectron2의 DeepLabV3+를 채택했다.
실험에서는 먼저 SAL 논문에 따라 모든 카메라를 단위 구 안에 있도록 표준화하고 네트워크 매개 변수를 초기화한다. 따라서 SDF는 단위구에 가깝고 구의 표면 법선은 안쪽을 향한다.
2D semantic 분할 및 장면 재구성을 위해 이미지의 크기가 640 × 480으로 조정된다.
Adam optimizer를 사용하고 50k 반복에 대해 1024개의 광선을 배치하여 네트워크를 훈련한다.
학습된 SDF에서 표면 mesh를 추출하기 위해 Marching Cubes 알고리즘을 사용한다.
Experiments
Datasets, metrics
ScanNet(V2) 및 7-Scene 데이터셋에서 실험을 수행한다.

ScanNet의 훈련 세트에서 2D semantic 분할 네트워크를 훈련하고 각각의 데이터셋에서 4개씩 총 8개의 장면에 대해 실험한다. 각 장면에는 1K~5K의 뷰가 있다. 재구성에서는 일률적으로 뷰의 1/10을 샘플링한다.
3D 재구성의 경우 RGB-D(depth) 융합 결과를 ground truth로 사용하고 5가지 표준 메트릭(accuracy, completeness, precision, recall, F-score)으로 평가한다. F-score를 종합적인 메트릭으로 간주한다.
Semantic 분할을 위해 바닥과 벽의 IoU를 평가한다.
Ablation studies
4가지 구성으로 훈련한다. 기본 VolSDF, Ld를 추가한 VolSDF-D, Lgeo를 추가한 VolSDF-D-G, VolSDF-D에서 추가적으로 3D 공간의 semantic을 학습한 VolSDF-D-S.

VolSDF-D-G를 보면 Lgeo가 확실히 평면을 깔끔하게 만드는 것을 볼 수 있다.
그리고 모든 부분에서 본 논문의 모델이 가장 뛰어나다.

Comparisons with the state-of-the-art methods
COLMAP*은 평면 피팅이 있는 MVS 방법.

COLMAP는 융합 단계에서 여러 보기 간에 일관성이 없는 재구성된 점을 걸러내기 때문에 매우 높은 정밀도를 달성할 수 있다. 그러나 이 프로세스는 리콜을 희생한다.
COLMAP*와 ACMP는 COLMAP보다 먼저 평면을 적용하여 일부 누락된 영역을 완료하고 더 높은 리콜을 달성할 수 있다. 그러나 이들의 최적화 전략은 추정된 깊이 맵의 일관성을 보장할 수 없어 노이즈가 많은 재구성을 초래한다.
볼륨 밀도 표현이 geometry에 대한 충분한 제약을 갖고 있지 않기 때문에 NeRF의 성능은 좋지 않다.

Semantic segmentation


마지막 행의 경우 벽의 밑단 부분이 바닥의 색과 똑같음에도 불구하고 꽤 좋게 분류한 것을 볼 수 있다.
Novel view synthesis
새로운 뷰 합성을 평가하기 위해 훈련 뷰에서 벗어나 새로운 뷰를 선택하고 이미지를 렌더링한다.

Conclusion
본 논문에서는 Manhattan-world 가정을 기반으로 한 새로운 실내 장면 재구성 방법을 소개했다. 주요 아이디어는 평면 영역의 semantic 정보를 활용하여 geometry 재구성을 돕는 것이다. 2D 분할 결과로부터 3D semantic을 학습하고 geometry와 함께 3D semantic을 공동으로 최적화하여 부정확한 2D 분할에 대한 견고성을 향상시킨다. 실험에 따르면 제안된 방법은 비평면 영역의 세부 정보를 유지하면서 정확하고 완전한 평면을 재구성할 수 있었으며, 공공 데이터 세트에서 SOTA 방법을 크게 능가했다.
이 연구는 Manhattan-world 가정만을 고려한다. Manhattan-world 가정을 따르지 않는 장면에 대해서는 손실 함수의 geometry 제약 조건을 수정 하여 다른 가정을 채택하도록 확장할 가능성 또한 있다.
'논문 리뷰 > etc.' 카테고리의 다른 글
| Can CNNs Be More Robust Than Transformers? 논문 리뷰 (0) | 2022.06.10 |
|---|---|
| When does dough become a bagel? Analyzing the remaining mistakes on ImageNet 논문 리뷰 (1) | 2022.05.22 |
| Thin-Plate Spline Motion Model for Image Animation (TPS) 논문 리뷰 (0) | 2022.05.11 |
| StyleGAN-Human 논문 리뷰 (0) | 2022.05.03 |
| Focal Sparse Convolutional Networks(FocalsConv) 논문 리뷰 (0) | 2022.05.01 |
| Masked Siamese Networks 논문 리뷰 (0) | 2022.04.20 |



