Diffusion Model Alignment Using Direct Preference Optimization (Diffusion-DPO)

[arXiv](Current version v1)

 

 

Abstract

Direct Preference Optimization(DPO)을 확산 모델에 적용한 Diffusion-DPO 제안

 

 

 

Background

Diffusion Models

Simple loss:

 

Direct Preference Optimization

조건 c에서 보상 모델 r이 접근할 수 있는 ranked pair x^win, x^lose에 대해 Bradley-Terry model은 인간 선호도를 다음과 같이 규정한다.

 

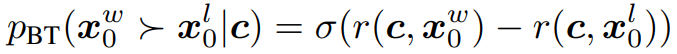
보상 함수는 신경망으로 매개변수화되고 maximum likeihood를 통해 훈련될 수 있다.

 

RLHF

보상을 최대화하는 동시에 KL-divergence를 통해 정규화된다.

 

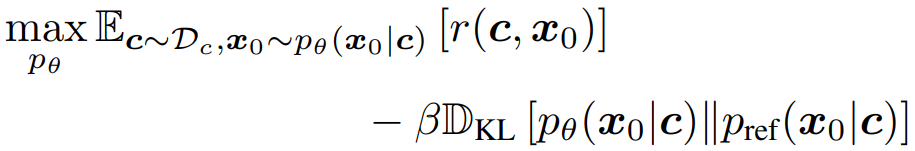
DPO Objective

위의 식에 대한 최적의 솔루션은 다음과 같은 형태를 취함. (참고)

 

Z(c)는 모든 샘플에 대한 합쳐진 확률이 1이 되도록 하는 정규화 term이고

 

최적 솔루션을 r에 대하여 정리하면 다음과 같다.

 

보상 함수를 사용하지 않고 분포를 직접 최적화하는 maximum likeihood 목적 함수를 작성할 수 있다.

 

 

 

DPO for Diffusion Models

분포 p_θ를 최적화하기 위해 DPO를 확산 모델에 적용할 때 모든 확산 경로 0~T를 주변화해야하므로 쉽지 않다. 따라서 evidence lower bound(ELBO)를 활용한다. 

 

모든 denoising chain의 보상을 R로 정의하여 보상 함수 작성.

 

KL-divergence term 추가.

 

DPO 목적 함수로 변환. (c 생략)

 

하지만 위 식은 일반적으로 T가 매우 크고 수많은 chain을 포함하므로 다루기 어렵다.

 

p_θ, p_ref를 역분해로 대체하고 Jensen's Inequality를 통해 기댓값을 밖으로 밀어내어 경사하강이 가능한 bound를 얻는다.

 

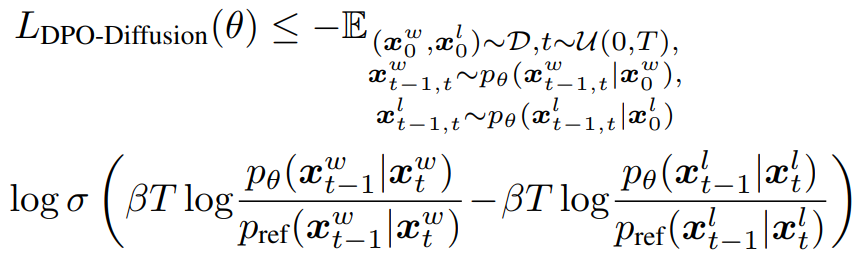
그러나 reverse joint p_θ(x_t−1, x_t|x₀, c)의 샘플링은 여전히 다루기 힘드므로 역방향 과정을 순방향 과정으로 근사한다.

 

p가 아니라 q를 통해 샘플링함 + negative log likeihood → KL-divergence 변환:

 

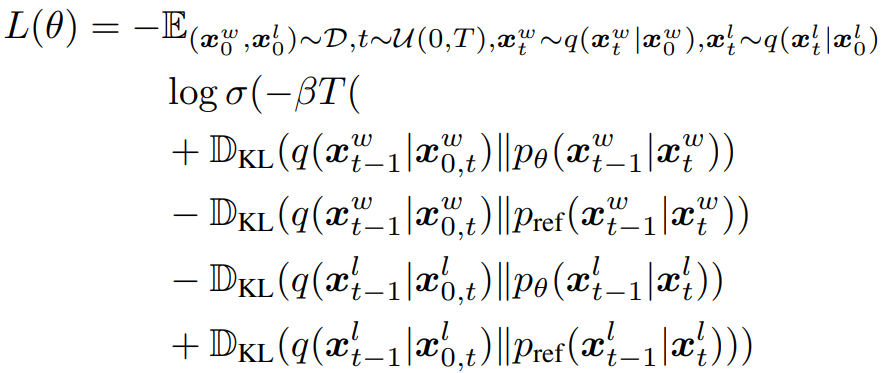
Simple loss로 단순화: 선호도로 학습되는 모델은 이전의 모델에 비해 winning sample을 더 잘 예측하고, losing sample을 예측하지 못하도록 훈련됨.

 

 

 

 

Experiments