[Github]
[arXiv](2024/02/06 version v1)
Abstract
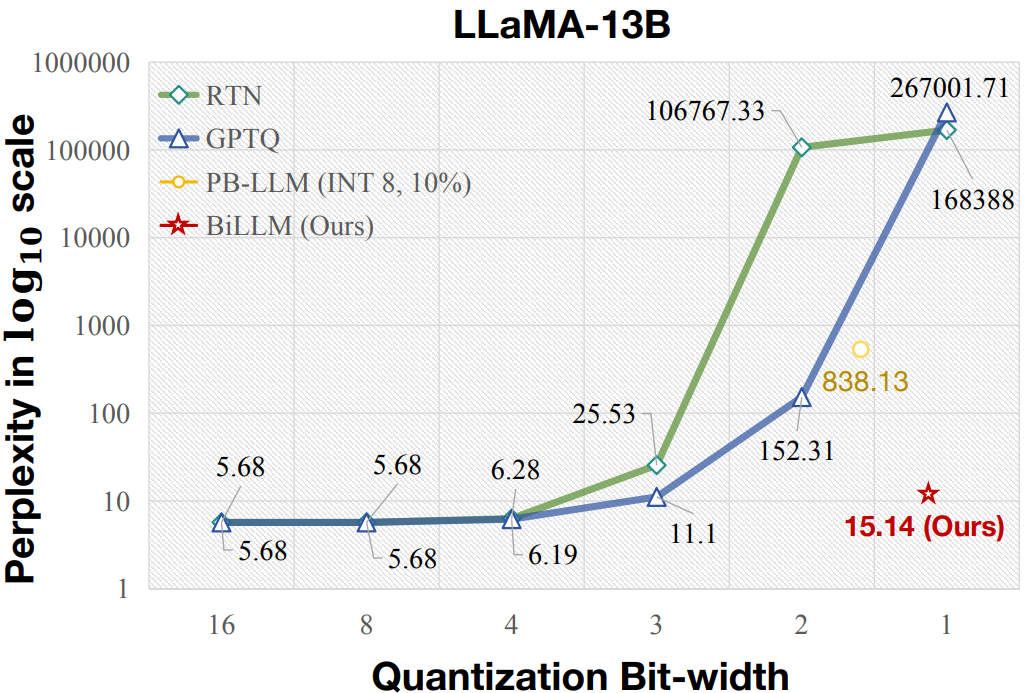
고정밀 추론이 가능한 1-bit post-training quantization (PTQ) 방식인 BiLLM 제안
Introduction
두 가지 중요한 관찰:
- 가중치의 Hessian matrix는 긴 꼬리 분포를 보인다.
- 가중치 크기의 density distribution은 종 모양 패턴을 따른다.
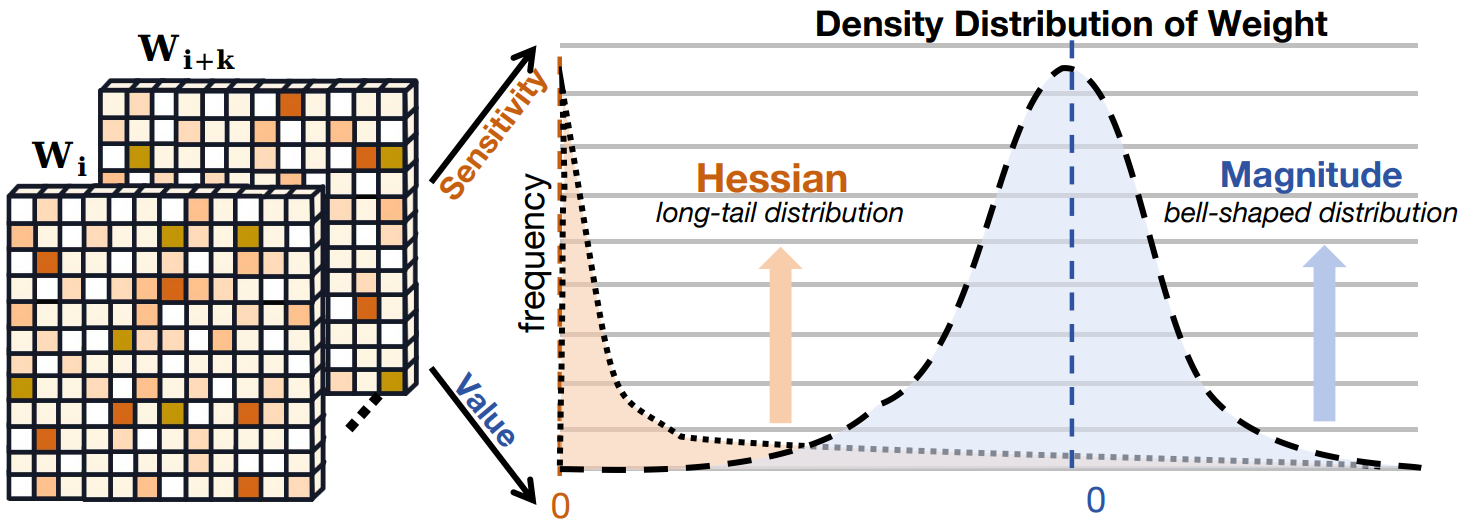
이는 대부분의 가중치가 중복적이고 소수의 가중치가 중요한 역할을 한다는 것을 의미하며 공격적인 양자화를 가능하게 한다.
두 가지 핵심 설계:
- Hessian matrix를 통해 유의미한 가중치의 복원을 극대화
- 비돌출 가중치에 대한 최적의 분할 이진화 전략
일반적인 네트워크 이진화:
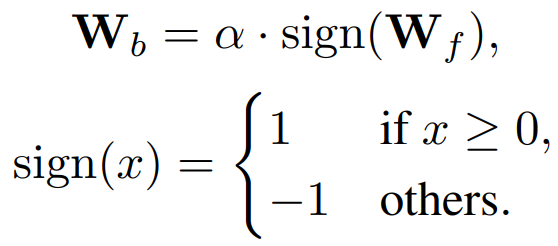 |
 |
Method
- Salient Weight Binarization for LLMs
- Bell-shaped Distribution Splitting for Binarization
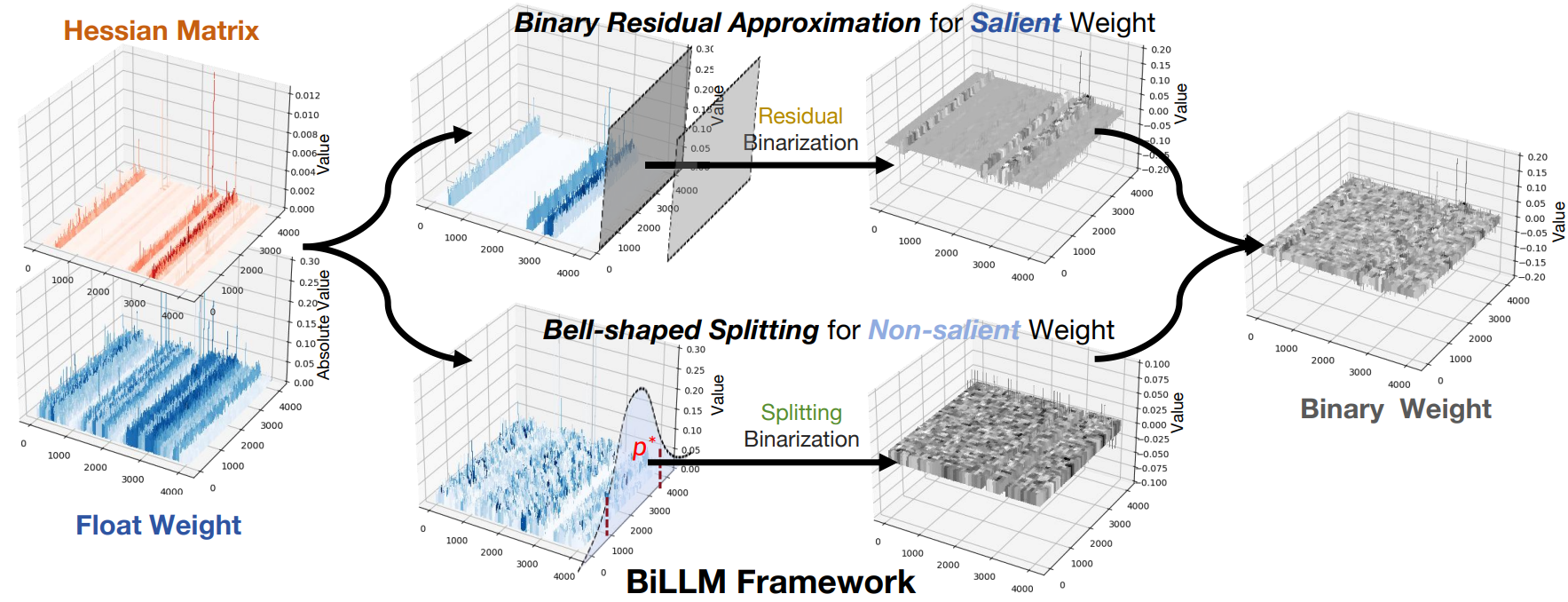
Salient Weight Binarization for LLMs
Hessian matrix는 민감도 측정을 위한 일반적인 벤치마크이다.
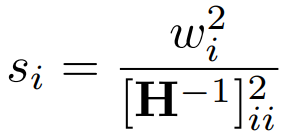
Structural Searching Selection
비구조적 선택을 사용하면 추가적인 인덱스를 위한 비트가 소모될뿐더러 이상치는 대부분 특정 행이나 열에 집중되어 있기 때문에 구조적 선택을 사용.
BiLLM에서는 가중치 행렬을 열 별로 분할하여 돌출성을 결정한다.
각 열에 대해 돌출성 내림차순으로 정렬한 뒤 양자화 목표는 다음과 같으며
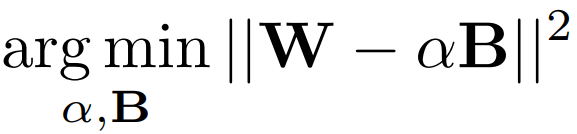

다음으로 설정하면 간단히 풀 수 있고
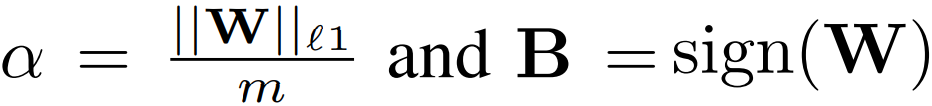
최적화 함수는 다음과 같다.
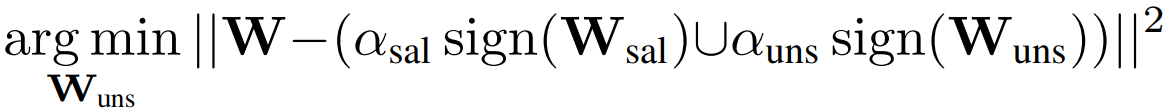
Binary Residual Approximation
돌출된 가중치를 보존하면 이진화의 이점이 약화된다. 양자화 오류를 최소화하며 이진화하기 위한 새로운 접근법.
이진화 후 잔차를 다시 이진화한다.
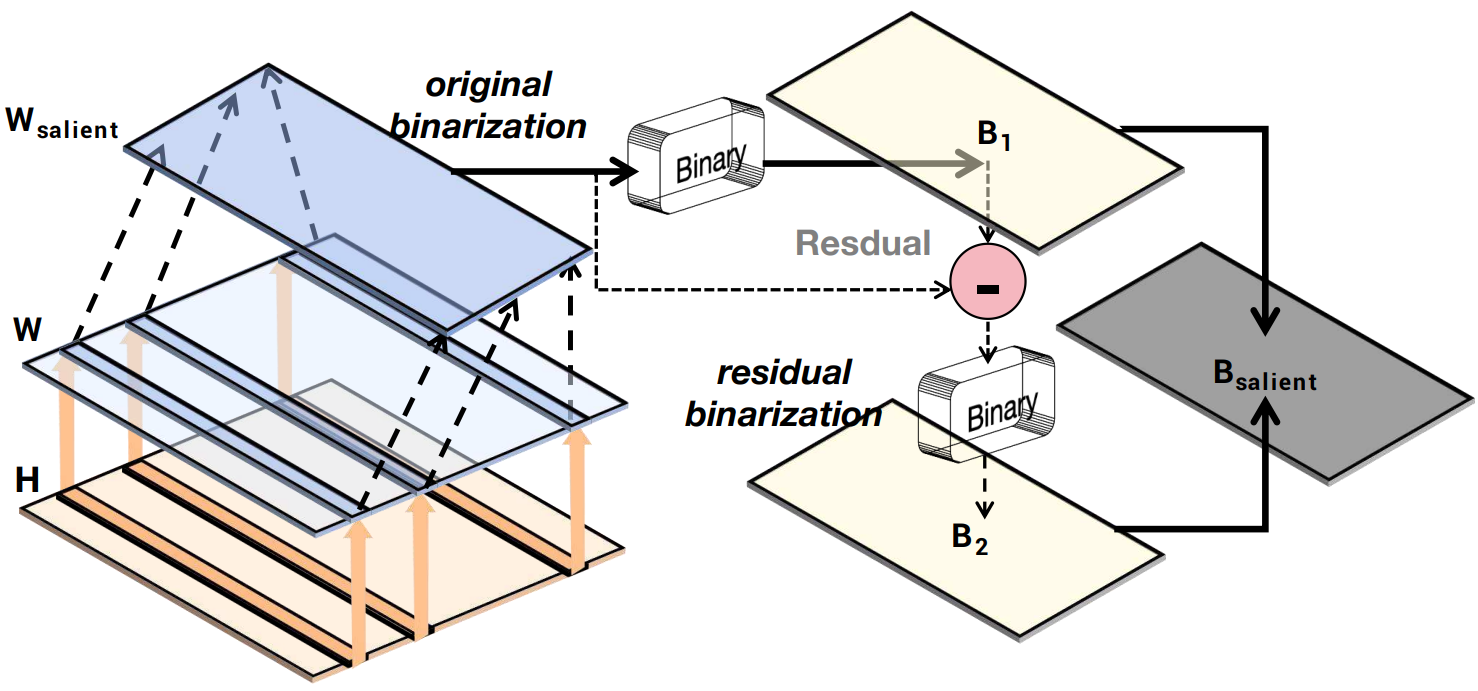
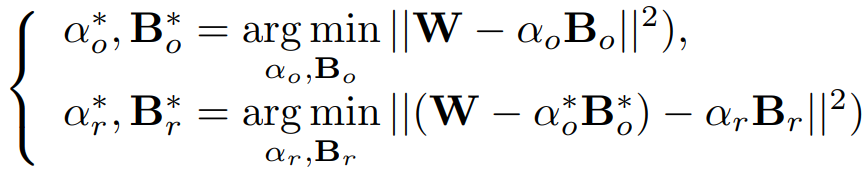
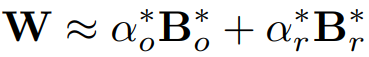
양자화 오류:
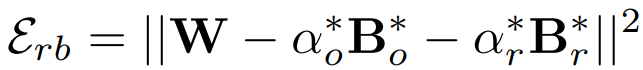
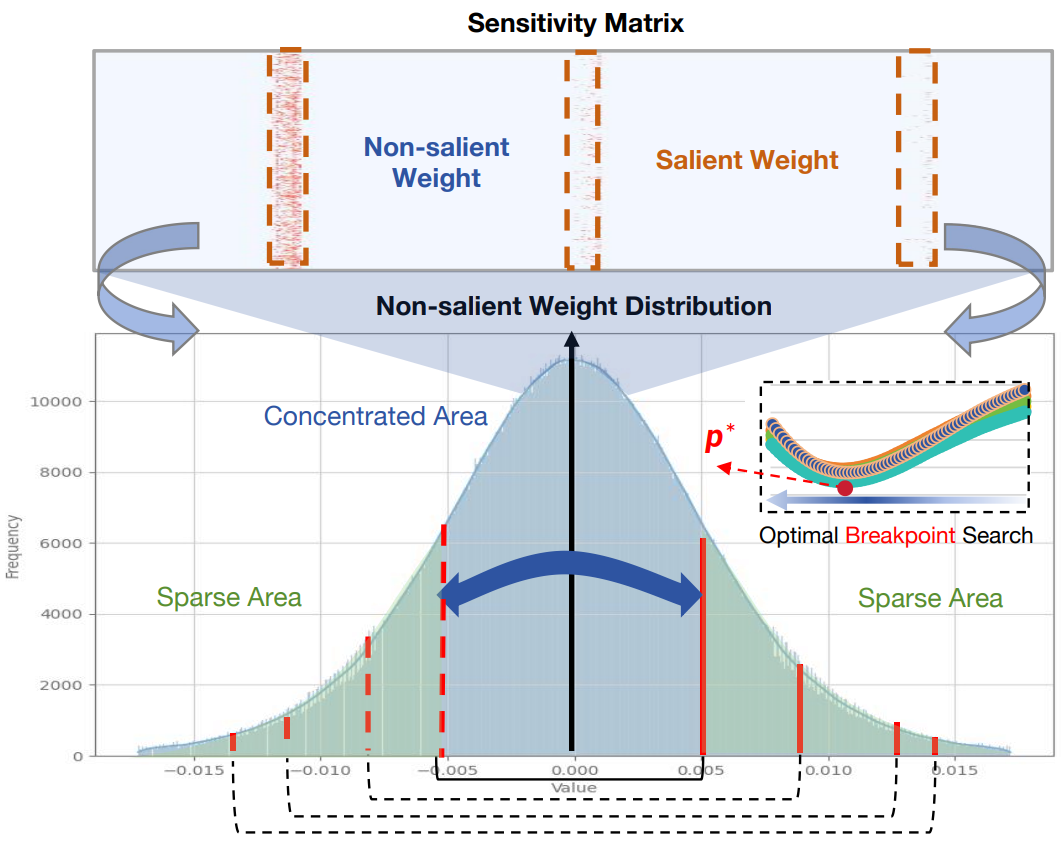
Bell-shaped Distribution Splitting for Binarization
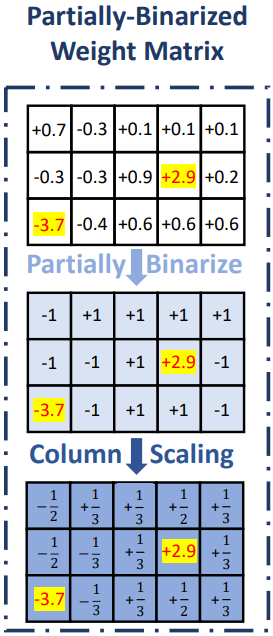
극단적인 이진 양자화는 많은 손실이 발생하기 때문에 추가적으로 group-wise 양자화를 사용한다.
나머지 비돌출 가중치를 다시 두 그룹으로 나누고 다른 scale로 양자화한다.
위 분포가 대칭인 확률 밀도 함수 g(x)라고 가정하면 양자화 오류는 다음과 같고
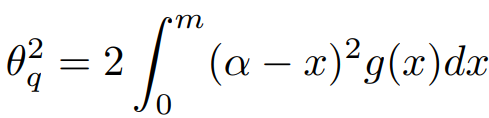
p로 분할하면
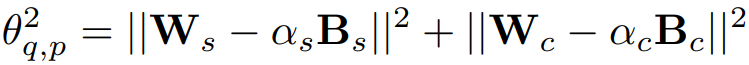
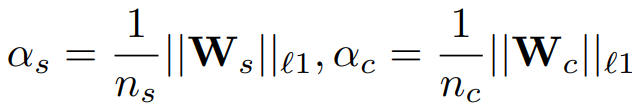
최적화 목표:
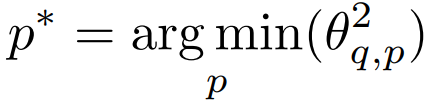
이상적인 가우스 분포를 따를 때, 이는 이전 연구에서 global minimum을 갖는 convex function임이 입증되었다.
실제로는 모든 열을 몇 개의 블록으로 나누고 각 블록에서 각 요소들을 잔차 오류 순으로 정렬한 뒤에 블록 내에서 최적의 중단점 p를 계산한다.
Experiments
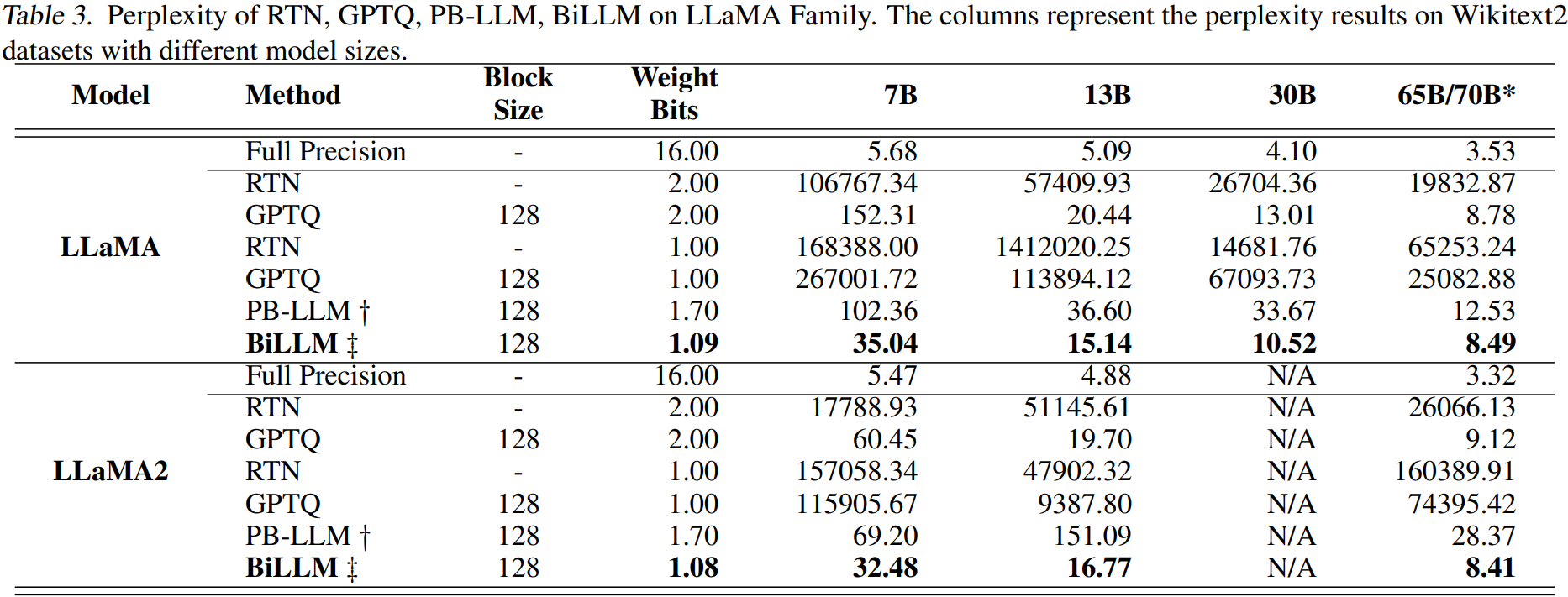
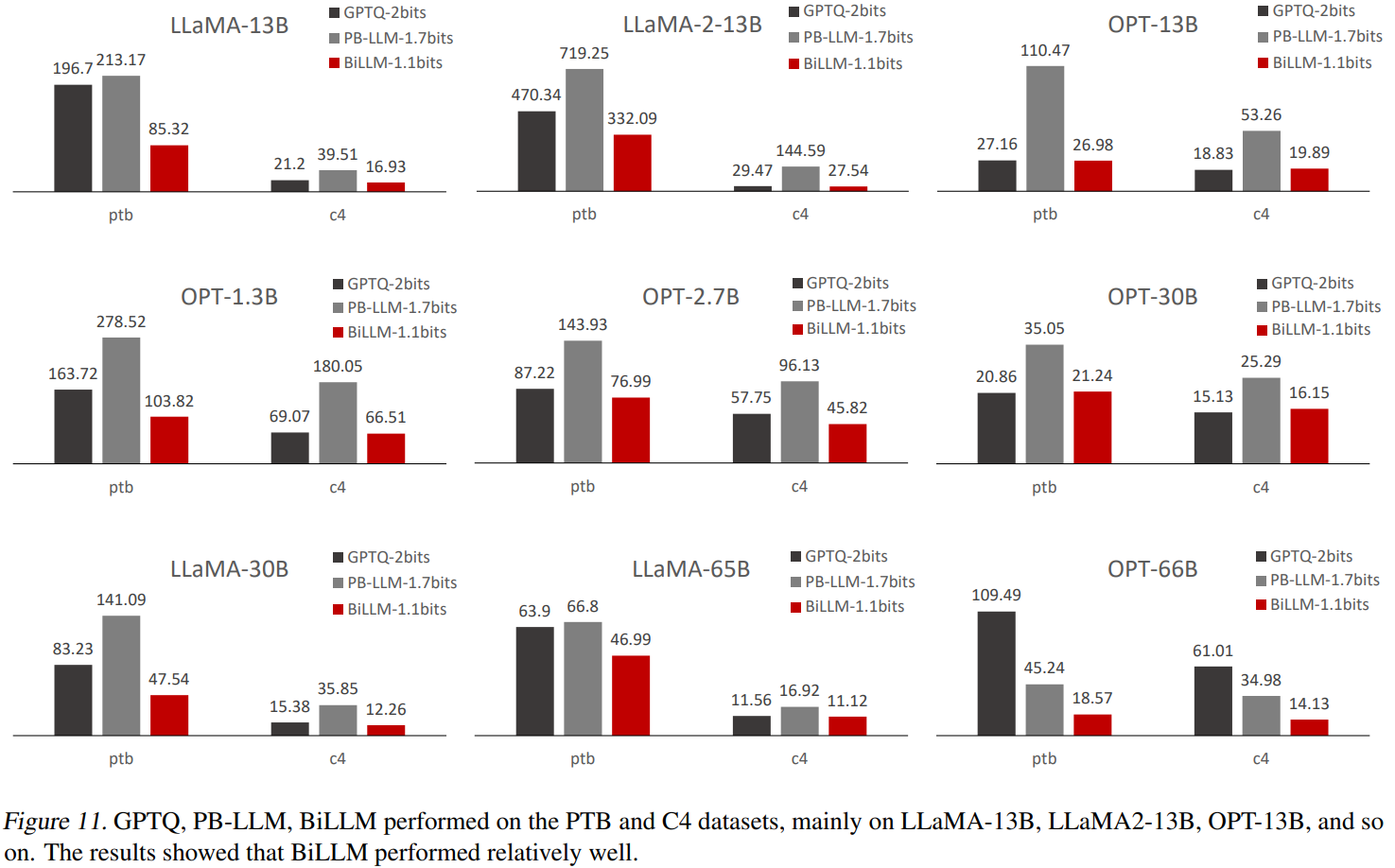
'논문 리뷰 > Language Model' 카테고리의 다른 글
| Chain-of-Thought Reasoning Without Prompting (CoT-decoding) (1) | 2024.02.26 |
|---|---|
| World Model on Million-Length Video And Language With RingAttention (LargeWorldModel) (0) | 2024.02.22 |
| More Agents Is All You Need (1) | 2024.02.21 |
| Self-Discover: Large Language Models Self-Compose Reasoning Structures (0) | 2024.02.20 |
| OpenMoE: An Early Effort on Open Mixture-of-Experts Language Models (1) | 2024.02.19 |
| ST-MoE: Designing Stable and Transferable Sparse Expert Models (1) | 2024.02.19 |



