Optimal Brain Compression: A Framework for Accurate Post-Training Quantization and Pruning (OBC)

효율적인 전역 양자화, 양자화∙가지치기 통합

 

[Github]

[arXiv](Current version v2)

 

 

Abstract

정확한 훈련 모델이 주어지고 적은 양의 교정 입력 데이터만을 기반으로 재훈련 없이 압축해야 하는 까다로운 one-shot/post-training 설정에서 DNN 압축 문제를 고려한다. 가지치기와 양자화를 통해 post-trining의 실용적 성능을 크게 개선하는 새로운 압축 프레임워크를 소개한다.

 

 

 

Introduction

기존 가지치기/양자화 방법들은 점진적인 가지치기와 재훈련이 필요하기 때문에 post-training 환경에 적용할 수 없었다.

 

전역 압축의 하위 문제인 layer-wise 압축에서 시작한다.

우리의 목표는 입력 X, 가중치 W에 대해 다음과 같은 압축된 Ŵ를 찾는 것이다.

 

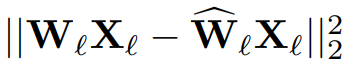
본 논문의 주요 기여는 위의 제곱 오류 공식의 계산 비용을 줄이는 일련의 알고리즘이다.

 

연구진이 개발한 Optimal Brain Quantizer(OBQ) 알고리즘은 가중치를 하나씩 양자화한 후 폐쇄형 업데이트를 적용하여 손실을 줄인다. OBQ를 이용한 통합 프레임워크를 Optimal Brain Compressor(OBC)라고 부른다.

 

 

 

Problem Definition and Background

The Layerwise Compression Problem

함수 f로 정의되는 각 레이어는 제약 조건 C를 만족하는 동시에 압축 손실을 최소화해야 한다.

 

이전 연구들에 따라 선형 레이어로 전개할 수 있는 선형 및 convolution 레이어 압축을 다루며 가중치는 W는 d*d 행렬, 입력 X의 차원은 d*N.

 

The Optimal Brain Surgeon (OBS) Framework

참고: 헤시안 행렬 H(의 근사인 fisher)를 이용한 가지치기 최적화

손실이 최소한으로 증가하는 가지치기 가중치 w와 그에 따른 각 가중치의 업데이트 δ.

 

OBS for Layer-Wise Pruning

OBS 프레임워크를 반복적으로 사용하여 가중치를 제거하는 것은 global 최적으로의 수렴을 보장하지는 않는다. 하지만 로컬 최적에서 결정을 내리기 때문에 효과적이다.

 

 

 

An Optimal Greedy Solver for Sparsity

이전 연구와는 달리 어떤 근사치에도 의존하지 않고 계산 비용을 줄임.

 

The ExactOBS Algorithm

각 레이어에 대한 최적화 문제를 가중치의 각 행에 대한 최적화 문제로 정의:

 

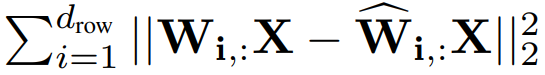
Step 1: Handling a Single Row

H는 각 행의 가중치 자체의 값과는 무관하고 가지치기한 인덱스에 대해서는 H의 행과 열을 제거하기만 하면 되므로, 실제로 H를 한 번만 계산하면 된다.

 

가지치기를 H의 역행렬에 반영하는 것도 가능하다. (증명은 부록 A.1)

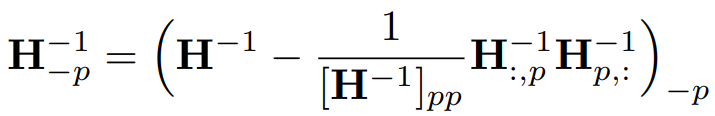
전체 알고리즘:

 

Step 2: Jointly Considering All Rows

각 행은 다른 행의 영향을 받지 않고 서로 독립적이므로, 각 행에서 가중치가 제거되는 순서는 정해져 있다. 또한 가중치를 차례대로 잘라내면서 모든 손실의 변화를 기록할 수 있다.

 

모든 행의 가중치 제거 순서와 손실의 변화를 알면, 전체 가중치의 global mask 또한 쉽게 결정할 수 있다. 

Global mask에 대해 각 행에서 그룹 OBS 최적화 공식으로 나머지 가중치를 업데이트한다.

---

Implementation Details

Hessian matrix가 잘 구해지지 않을 경우 대처:

• 데이터 샘플이 부족했다. → 데이터를 추가하여 적은 비용으로 hessian matrix에 누적할 수 있음.
• 입력 데이터가 선형 종속 → hessian matrix의 대각에 완충 항을 추가

 

소규모 CUDA 호출이 많으므로 여러 행을 동시에 처리하여 오버헤드 절약.

 

N:M Sparsity, Block-Sparsity

N:M Sparsity의 경우 그냥 M개 중에서 N개 뽑으면 됨.

Block-Sparsity의 경우 oBERT랑 똑같이 하면 됨.

 

 

 

The Optimal Brain Quantizer (OBQ)

The Quantization Order and Update Derivations

OBS를 양자화에 활용한다.

OBS 라그랑지안의 목표인 -w_p를 

다음으로 변경,

 

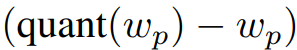
-w_p는 최적화 과정 내내 상수로 존재하므로 계산할 필요 없이 결과에서 대체하기만 하면 된다.

 

Quantizing Full Layers

손실 변동이 가장 작은 인덱스를 제외한 다른 가중치는 동시에 양자화하지 않는다. 다른 가중치가 업데이트됨으로써 양자화 오류를 보상하여 전체적인 양자화 결과가 더 좋아질 수 있기 때문이다. 이전 챕터의 알고리즘 1에 양자화를 연결하여 가지치기와 통합할 수 있다. (언급은 안돼있지만 양자화/가지치기 후에 해당 인덱스는 고정할 듯)

 

Quantization Outliers

이상치는 양자화 오류가 크므로 보통 마지막에 양자화되는데, 중간 가중치 업데이트에 의해 밖으로 밀려나 더 악화될 수 있다. 이를 방지하기 위해 양자화 전, 후의 차이가 ∆/2를 넘는 경우 순서에 상관없이 즉시 양자화한다.

(참고: Quantization step size ∆ )