SparseGPT: Massive Language Models Can Be Accurately Pruned in One-Shot

Inverse hessian matrix 재사용, 유효한 가중치만 업데이트

 

[Github]

[arXiv](Current version v3)

 

 

Abstract

매우 큰 모델 규모에서 효율적으로 작동하는 최초의 one-shot 가지치기 방법인 SparseGPT 제안

 

 

Introduction

Approximate sparse regression solver를 통해 가지치기 문제를 해결한다. 50~60%의 가지치기를 시행해도 정확도가 조금밖에 떨어지지 않는다.

 

큰 모델일수록 희소성을 도입해도 성능이 떨어지지 않는다.

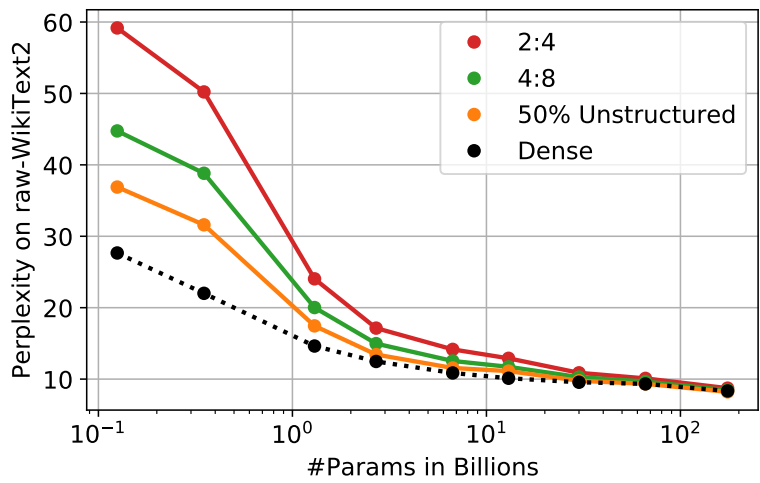
또한 본 논문에서 제안하는 기술은 양자화와 함께 사용될 수도 있다.

 

SparseGPT의 주목할만한 속성 중 하나는 각 레이어의 입력-출력이 보존되도록 설계되어 완전히 로컬이라는 것이다.

 

 

 

The SparseGPT Algorithm

Fast Approximate Reconstruction

Motivation

Hessian matrix의 반전을 통해 가지치기에서 최적값을 찾을 수 있다.

(참고: 헤시안 행렬 H(의 근사인 fisher)를 이용한 가지치기 최적화)

 

Different Row-Hessian Challenge

각 행에 대하여 H의 계산이 필요하기 때문에 계산 복잡성이 매우 높다. 효율적인 알고리즘을 설계하는 핵심은 H를 재사용하는 것에 있다.

 

Equivalent Iterative Perspective

고정된 마스크 m에 대한 최적의 OBS 업데이트와 그에 대한 오차:

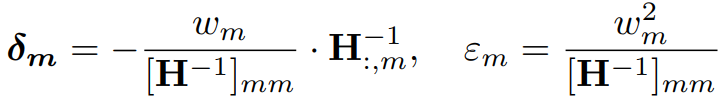
OBS 업데이트를 반복적으로 사용하여 회귀적으로 재구성할 수 있다.

 

Optimal Partial Updates

OBS 업데이트에 대해 모든 가중치를 조정하지 않고 현재 마스크 M에서 가지치기되지 않은 가중치 집합 U에 대해서만 업데이트하면 안 될까? H_U를 사용하여 w_U만 업데이트하면 조정할 수 있는 가중치가 적기 때문에 오류 보상이 효과적이지 않을 수 있지만 OBS 업데이트는 여전히 최적이라고 한다.

 

Hessian Synchronization

다음과 같이 시퀀스 U를 정의: (d_col = 행의 길이 = 열의 개수. 이거 좀 헷갈림)

 

H_U^-1는 한 번 계산하면 W의 모든 행에 공유되며, H_U의 열과 행의 제거에 대해서는 가우스 소거법을 통해 H_U^-1에 반영할 수 있다. (가우스 소거법에 대한 자세한 설명은 OBC 논문의 부록 참조)

 

정리된 가중치에 대해 업데이트하지 않기 위해 지나간 열은 업데이트에서 배제한다.

(계산은 각 행에서 따로 진행되고, 처음 계산한 H_U^-1는 모든 계산 과정에서 사용됨.)

 

Adaptive Mask Selection

고정된 마스크가 아닌 동적 마스크의 경우, 각 열에서 가지치기 쉬운(손실 변동이 작음) n개의 가중치를 선택하여 가지 치는 방법이 일반적이다. 그러나 이러한 방법은 모든 열에서 제거된 가중치 개수가 같아야 하는 추가적인 구조 제약이 부과되는 것과 같다. 대규모 언어 모델의 경우 이러한 제약 조건에 특히 민감하다.

 

문제를 해결하기 위해 입력 차원(열 개수)을 블록으로 나누고 OBS 업데이트 오류를 기반으로 블록 내에서 가지치기 쉬운 p%의 가중치를 잘라낸다. (참고: OBC)

 

Full Algorithm Pseudocode

SparseGPT와 비슷한 구조인 [GPTQ]의 모든 최적화 방법 통합:

이걸로 이해 못함 그냥 링크 보삼~

 

Joint Sparsification & Quantization

또한 추가 비용 없이 가지치기와 양자화를 결합할 수도 있다.