Hessian matrix를 효율적인 fisher matrix로 근사하여 가지치기에 활용
[Github]
[arXiv](Current version v5)
Abstract
Hessian- or Inverse-Hessian-vector product 형태의 2차 미분 정보는 최적화 문제를 해결하기 위한 기본 도구이다.
Inverse-Hessian matrix의 효율적인 추정치를 계산하기 위해 WoodFisher라는 방법을 제안한다.
Introduction
DNN을 압축하기 위한 최근 연구는 고전적인 Optimal Brain Damage/Surgeon 프레임워크에서 그 뿌리를 찾을 수 있다. 대략적으로 제거할 최적의 피라미터를 찾기 위해 테일러 전개 기반으로 로컬 2차 모델 근사를 구축하는 것이다.
핵심은 Inverse-Hessian-vector product(IHVP) 이다. 하지만 대형 모델에 2차 방법을 적용하기 힘드므로 근사를 통해 수행되는 경우가 많지만 그러한 근사의 품질과 확장성에 대해서는 알려진 바가 없다.
먼저 WoodFisher라고 부르는 Woodbury matrix identity와 함께 사용되는 2차 근사 방식을 검토하고, 가지치기 방법에서 어떻게 사용되는지 보여준다.
WoodFisher의 유용한 기능
- 레이어별 희소성 목표를 수동으로 선택할 필요가 없다.
- 제한된 데이터 체제에서 압축을 적용할 수 있다.
- 로컬 2차 모델의 1차 gradient term을 고려할 수 있다. (WoodFisher의 확장인 WoodTaylor, 최하단에 있음)
Background
Deterministic Setting
훈련 세트 S = {(xi, yi)}에서 가중치 w를 통해 x를 y로 만드는 함수 f(x;w) = y를 학습하는 게 목표이다.
(w는 din → dout 선형 매핑의 한 행인 din → 1 매핑 가중치를 나타내고, y의 길이는 1이 아니라 dout인 것 같음. 아마...?)

loss function: (저 화살표는 매핑함수라고 합니다)
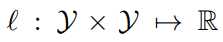
Training loss:
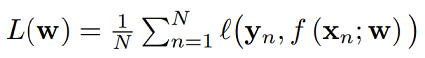
The Hessian Matrix
두 번 미분가능한 L에 대하여 헤세 행렬 H와 w 및 그 주변 δw에 대하여 근사를 구축할 수 있다.
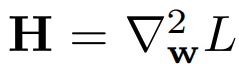
이는 손실에 대한 로컬 2차 모델이라고도 하며 다음과 같다.

Probabilistic Setting
2차 모델 대신 대안적인 공식은 결합 분포를 이용하는 것이다.
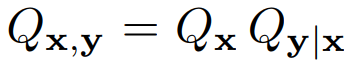
Qx는 훈련 세트 입력의 분포 Q̂x로 잘 추정할 수 있으며, Qy|x는 모델을 통해 Py|x로 대체한다.
이러한 조건부 분포 사이의 KL divergence를 이용해 훈련 목표를 공식화하면: p(y|x)가 1이 돼야 함

The Fisher Matrix
참고 : Hessian matrix와 Fisher matrix
Hessian matrix와 fisher matrix는 w와 관련된 곡률을 나타내는 거의 비슷한 개념이며, 모델이 완벽하다는 가정하에 hessian과 동일하다. Fisher matrix가 더 계산이 쉬워서 hessian 대신 fisher를 문제를 푸는 데 이용한다고 한다.

The Empirical Fisher
실제 설정에서, 실제 분포를 알 수 없으므로 경험적 근사치를 고려한다.
모델 분포 P를 경험적 훈련 분포 Q̂y|x로 대체하고 detetministic setting과 연결한다.

이 논문에서 특정 훈련 예제 (xn, yn)에 대한 손실을 ln로 표기한다.
Efficient Estimates of Inverse-Hessian Vector Product
The (Empirical) Fisher and the Hessian: A Visual Tour
CIFARNet에서 hessian과 경험적 fisher의 차이 시각화.

The WoodFisher Approximation
The Woodbury Matrix Identity
참고 : 행렬식 보조 정리, Sherman–Morrison-Woodbury formula(= Woodbury ID)
경험적 fisher를 다음과 같은 반복으로 표현할 수 있다.

Sherman–Morrison formula를 통해 역행렬을 구할 수 있다:

마지막으로,

Hessian 대신 경험적 fisher를 사용하고, Woodbury ID를 통해 그 역을 계산하는 이러한 방법을 WoodFisher라고 명명한다.
Computational Efficiency and Block-wise Approximation
실제로 이 방법에 일반적으로 100~400의 예제 집합이 필요하다.
대형 모델의 경우, 여전히 런타임이 과도하기 때문에 제한된 크기의 블록에서 대각 성분만을 추정하는 block-wise approximation을 사용해야 하며, 이는 hessian이 대각선으로 지배적인 경향이 있기 때문에 유효하다.
Model Compression
제거 시 훈련 손실이 최소한으로 증가하는 피라미터를 가지치기하는 아이디어에서 시작한다.
Dense weight w, 가지치기 후의 가중치 w + δw에 대해 δL을 최소화하려고 한다.

보통 네트워크가 로컬 최적(학습 완료된 상태)에서 가지치기되어 첫 번째 항은 제거되고 다음과 같이 단순화된다고 가정하는 경우가 많다.

Removing a single parameter wq
d차원 벡터인 w에서 q 인덱스의 값을 0으로 만들려는 경우를 다음과 같이 공식화할 수 있다.

왼쪽: 손실을 최소화하는 섭동 δw를 찾아야 한다.
오른쪽: 해당 섭동은 q인덱스의 값을 0으로 만들어야 한다. (eq는 q 인덱스가 1인 기저 벡터)
또한 이렇게 구한 최소 손실 중에서도 최솟값을 가지는 q 인덱스를 찾아야 하지만
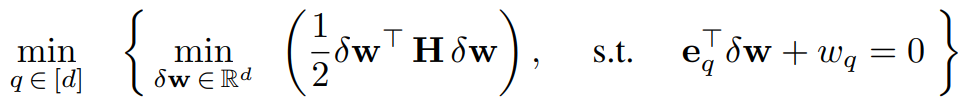
일단 먼저 내부의 최소화 문제에 집중한다.
제한 조건이 있는 최소화 문제를 라그랑주 승수법을 통해 다음과 같이 표현할 수 있다.

라그랑지안의 극한값인 Lagrange dual function g(λ)은 L'(δw, λ) = 0 에서 얻은 δw를 다시 대입하여 얻을 수 있다.
(미분 시 벡터의 전치는 신경 쓰지 않는 듯하다. xT = x)

g(λ)를 최대화하는 λ가 원래의 최적화 문제를 최소화하는 최적 값 λ*이다. 미분하여 간단히 구할 수 있다.
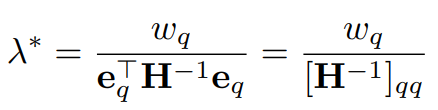
대입하여 δw, δL 구함:

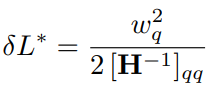
각 인덱스 q에 대해 δL을 내림차순으로 정렬하고 가장 낮은 인덱스를 가지치기하면 끝.
(H는 위에 설명한 경험적 fisher로 근사)
Removing multiple parameters at once
두 개의 피라미터를 제거하는 경우:
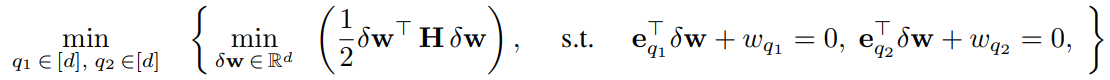
라그랑주 승수법:

Lagrange dual function: (단일 공식과의 구분을 위해 g'로 표기, 방법은 같음)


미분하여 연립방정식 풀면 됨:

Discussion
하지만 위 방법은 다루기가 어렵기 때문에 단일 인덱스에 대한 내림차순 정렬에서 가장 낮은 인덱스들을 가지치기하여 근사할 수도 있다. 이때 각 인덱스에 대한 섭동 δw를 추가하고 제거된 인덱스의 가중치는 0으로 한다. (서로의 섭동으로 0이 아니게 되기 때문에)
WoodTaylor: Pruning at a general point
지금까지 우리는 로컬 최적점에서 가지치기를 한다고 가정하였다. 하지만 계산에 1차 gradient를 통합하여 로컬 최적점이 아닌 일반적인 지점에서 가지치기를 수행할 수 있고, 그러면 동적 가지치기처럼 훈련 중에 가지치기를 수행할 수도 있다.

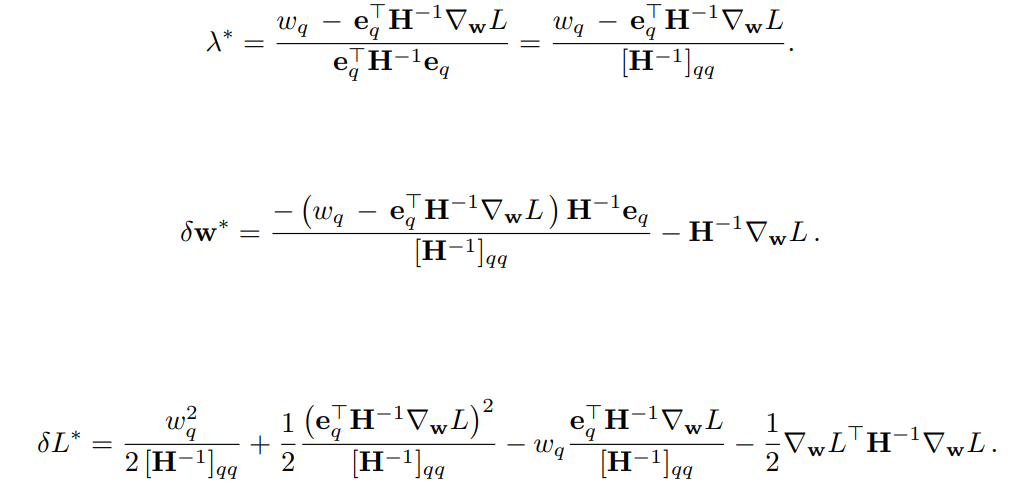
q와 무관한 마지막 항을 제거하여 최종적인 가지치기 통계량 얻음.




