[arXiv](Current version v2)
Abstract
훈련 단계에서 GPU 가속의 이점을 얻을 수 있는 Transposable-Fine-Grained Sparsity Mask
패턴이 다른 희소 구조에 대한 적응 방법인 AdaPrune
Introduction
DNN(Deep Neural Network)의 압축에는 양자화, 증류, 가지치기 등의 방법이 있다.
가지치기는 두 가지로 분류할 수 있다:

Nvidia는 모델 가중치를 fine-grained 2:4 희소 구조로 가중치를 마스킹한 뒤 재훈련하는 방법을 제안했다. [논문 리뷰]
하지만 이 방법은 훈련된 dense model이 필요하다는 단점이 있다.
[NM-Sparsity]에서는 forward 중 실시간으로 가지치기를 하고 STE로 backward를 수행해 모델을 두 번 훈련할 필요 없는 방법을 제안했다. 이때 마스크된 가중치에 대한 backward gradient를 줄이는 정규화 term이 추가된 SR-STE를 사용하였다.
본 논문의 기여:

- 희소 마스크 유형의 순위를 매기기 위한 측정 방법인 mask diversity 제안
- Backward pass에는 다음과 같이 전치된 행렬을 사용해야 한다.
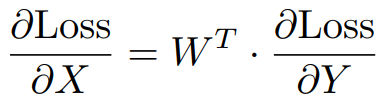
하지만 전치 행렬은 W와 같이 N:M 구조를 갖고 있지 않으며 GPU의 희소 행렬곱 가속화를 사용할 수 없다. 따라서 backward pass에서도 가속 가능한 transposable-fine-grained sparsity mask 제안.

- 재교육 없이 희소 마스크 유형을 변경할 수 있는 Adaprune 제안
Mask Diversity
구조적인 제약으로 인해 정확도가 저하된다는 가설에서 시작하여 특정 구조가 모델을 얼마나 제한하는지 정량화하기 위해 4가지 구조 제약 조건에서 MD를 측정 (수식이 있긴 한데 이걸 어떻게 설명해야 할지 참 어렵다...)
- Unstructured sparsity
- N:M sparsity
- Transposable N:M sparsity
- Sequential N:M sparsity : 모든 M 블록은 N 크기의 순차적 0을 포함해야 함 (압축이 쉬워 하드웨어 친화적)
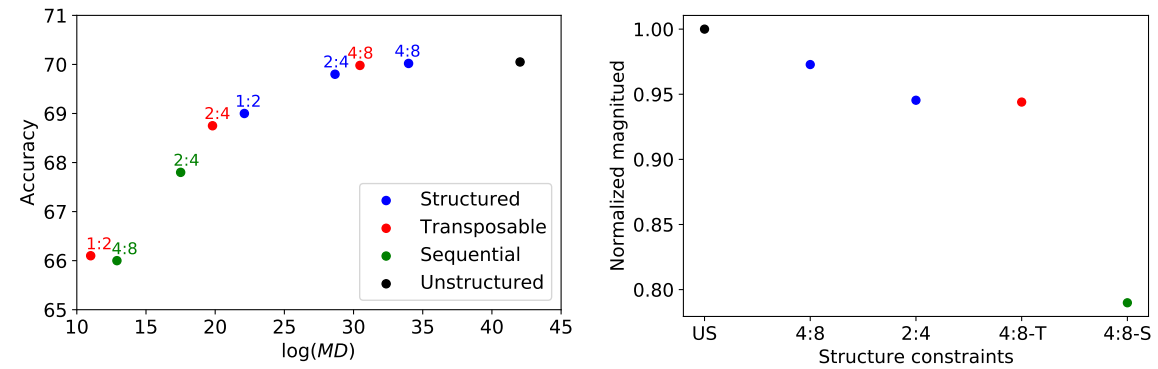
본 논문에서는 2:4 희소 구조보다 조금의 하드웨어 부담(3:1 → 5:1 multiplexer)이 더 있기는 하지만 2:4 structured와 MD, 정확도, L1 norm(dense model의 성능을 유지하면서 가지치기를 하기 위해 L1 norm을 최대화하여야 함)이 비슷한 4:8-T를 사용하기로 하였다.
Computing transposable sparsity masks
Problem formulation
우리의 목표는 WT의 행, 열(양방향)에서 N개의 요소를 마스킹 한 후 L1 norm을 최대화하는 것이다.


Reduction to Min-Cost Flow
이제 그 마스크를 어떻게 구할꺼냐는 문제인데...
위의 식을 다음과 같은 min-cost flow problem으로 만들 수 있다고 한다...

솔직히 뭔소린지 잘 모르게슴... 이건 제 수학 지식수준을 벗어난 것 같습니다... (빤스런)
2-Approximation algorithm
뭐 어쨋든 위에 설명한 최적의 방법은 계산 비용이 매우 많이 든다고 한다...
그래서 근사를 이용한 방법으로 비용을 줄인다고 하는데...
저는 잘 모르겠슴다...
Structured sparsity without full training
예를 들어, 4:8 희소 구조로 훈련된 모델을 배포하려는데 하드웨어에서 2:4만 지원하는 경우, 4개의 값 중 값이 작은 2개의 값을 가지치기해야 하는데, 4:8에서 가지치기되지 않았던 값이 가지치기될 수도 있다. 이러한 경우를 '패턴 위반'이라고 하고, 격차를 해소하기 위한 두 가지 방법에 대해 논의한다.
Fixing pruning bias using mean absorption
가지치기된 가중치의 평균으로 그렇지 않은 가중치의 통계값 조정 (이 논문의 Bias-Correction 참고)
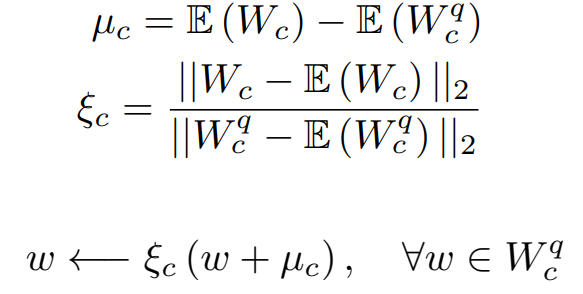
AdaPrune
원본 가중치 W와 찾고자 하는 가중치 W', 가중치 희소 마스크 S에 대해 다음과 같은 최적화를 수행한다.
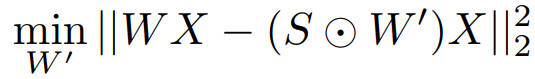
비교:
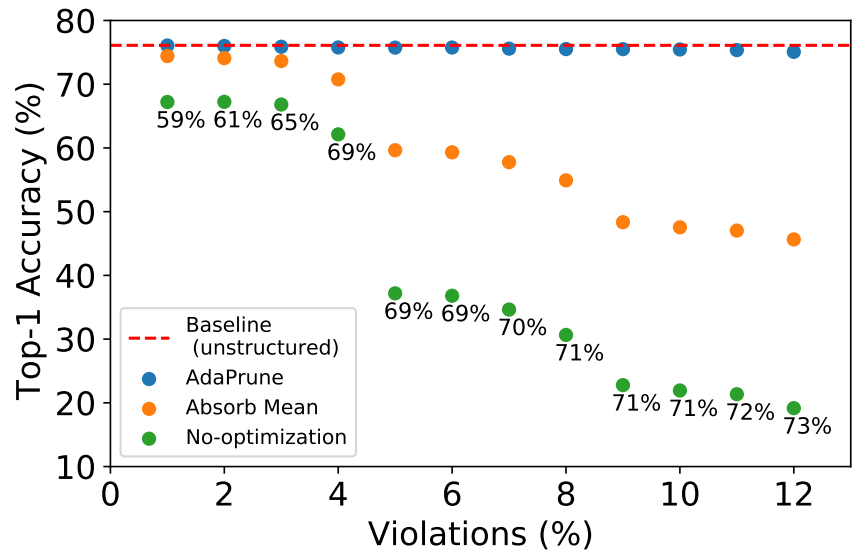
AdaPrune도 10% 내외의 패턴 위반에 대해서만 효과적이며, 높은 패턴 위반에는 전체 훈련이 필요하다.



