Consistency Models

OpenAI에서 공개한 자기 일관성을 통해 학습하는 모델

One-step으로 꽤 괜찮을 품질의 이미지를 생성할 수 있는 것이 인상적.

 

Github

arXiv

 

Abstract

확산 모델은 많은 진전을 이루었지만 느린 샘플링 속도와 반복 생성 프로세스에 의존한다.

이러한 한계를 극복하기 위해 Consistency Model(일관성 모델) 제안.

 

일관성 모델은 one-step 생성을 지원하면서도 품질을 위해 few-step 생성 또한 가능.

사전 훈련된 확산 모델을 증류하는 방법 또는 독립 실행형 생성 모델로 학습할 수 있다.

 

 

 

Introduction

확산 모델은 GAN처럼 학습이 불안정하지 않고 자동회귀 모델, VAE, Normalizing Flow와 같이 아키텍처에 제약을 부과하지도 않는다.

 

단점은 많은 반복 프로세스로 인한 비용과 시간의 문제.

 

본 논문의 목적은 반복 정제의 이점을 희생하지 않고 single step 생성이 가능하며 품질과 컴퓨팅 비용을 trade-off 할 수 있는 기능과 제로샷 편집 기능을 수행할 수 있는 생성 모델을 만드는 것이다.

 

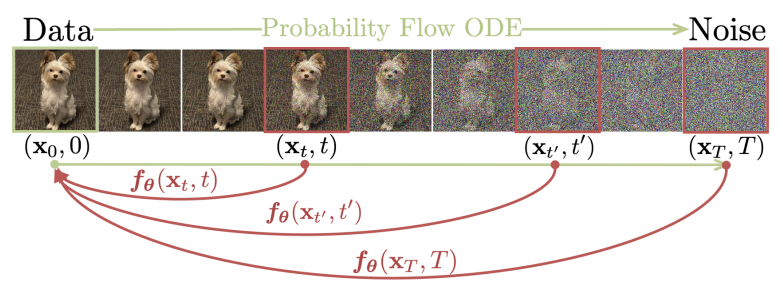
일관성 모델은 probability flow ODE 위에 빌드된다.

위의 궤적에서 timestep의 어떤 지점을 궤적의 시작 지점에 매핑하는 모델을 학습하며, 주목할만한 점은 동일한 궤적의 어떤 지점이든 항상 동일한 시작점에 매핑되는 자기 일관성이다.

 

사전 훈련된 확산 모델의 궤적에서 인접한 점 쌍을 생성한 뒤 이러한 쌍에 대한 모델 출력의 차이를 최소화하는 방법 또는 완전히 독립적인 방법으로 학습할 수 있다.

 

 

 

Diffusion Models

참고자료:

Score-based model, SDE, ODE, diffusion model의 발전 과정(글, 영상)

확산 모델 공부 자료 모음

Elucidating the Design Space of Diffusion-Based Generative Models

---

확산 모델은 p_data(x)를 SDE를 통해 확산하는 것으로 시작한다.

 

Stochastic differential equation (SDE)

 

좀 더 결정론적인 확산을 위한 PF ODE

Probability flow ordinary differential equation(PF ODE)

 

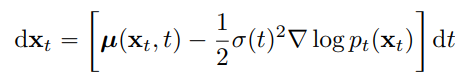
Empirical PF ODE

샘플링을 위해 score model을 학습하고

모델을 이용해 다음과 같은 경험적 추정치를 얻을 수 있음.

---

경험적 PF ODE를 초기화하기 위해 가우시안 분포로부터 x̂_T를 샘플링하고 수치적 ODE solver(Euler, Heun)를 통해 궤적 {x̂_t}를 얻음.

 

수치적 불안정성을 피하기 위해 매우 작은 값 ε(e.g. 0.002)에서 solving을 멈춤.

 

확산 모델의 느린 샘플링 속도를 개선하기 위해 DPM-solver ++ 등 다양한 방법들이 제안되었다.

하지만 ODE-solver들은 계산 비용이 많이 들고, 가장 비용이 적게 드는 방식은 점진적 증류 방식이었다.

점진적 증류

 

 

 

Consistency Models

Definition

궤적 {x_t}가 주어졌을 때 자기 일관성을 가진 일관성 함수를 정의한다.

일관성 함수는 동일한 궤적의 데이터 포인트에 대해 다음을 만족한다.

 

다음 그림과 같이 f_θ로 표시된 일관성 모델의 목표는 일관성 함수 f를 추정하는 것이다.

 

Parameterization

f(⋅, ε)은 항등함수이며 이 제약 조건을 경계 조건(boundary condition)이라고 한다.

 

심층 신경망 F_θ(x,t)를 통해 경계 조건을 구현하는 두 가지 방법:

• 간단한 방법

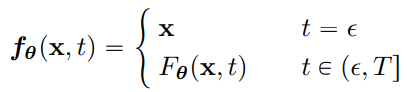
• 잔차 연결을 사용하여 피라미터화(c_skip(ε) = 1, c_out(ε) = 0인 미분 가능 함수)

미분 가능한 두 번째 방법 사용.

 

Sampling

초기 노이즈에서 일관성 모델의 단일 step으로 샘플 생성.

노이즈 제거 및 주입을 번갈아가며 다단계로 샘플링을 진행할 수도 있다.

 

+zero-shot 편집에 중요한 application:

알고리즘 1에서 greedy algorithm과 ternary search를 통해 FID를 최적인 지점을 찾는다.

 

Zero-Shot Data Editing

일관성 모델은 잠재 변수 모델과 비슷하게 잠재 공간의 샘플 간의 보간을 쉽게 할 수 있고 다양한 노이즈 레벨에 대응할 수 있다. 또한 확산 모델과 반복과 유사한 대체적인 절차를 통해 제로샷 문제를 해결하는 데 유용하다.

 

 

 

Training Consistency Models via Distillation

사전 훈련된 score model s_Φ(x,t)를 증류하는 것에 기반한 일관성 모델 훈련을 위한 첫 번째 방법 제시.

 

Elucidating the Design Space of Diffusion-Based Generative Models에서 제안한 공식(16:40부터)으로

다음과 같은 ODE step을 얻고 (확산 timestep 아님)

 

ODE solver를 통해 x_tn+1에서 x_tn^Φ를 추정할 수 있다.

 

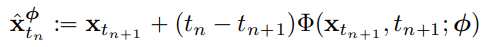
본 논문에서는 1단계 ODE solver만을 다룸.

---

데이터 x에 노이즈가 추가된 분포에서 x_tn+1을 샘플링하고 ODE solver를 통해 x_tn^Φ를 계산하여 인접한 한 쌍의 데이터 포인트(x_tn^Φ, x_tn+1)를 생성할 수 있고 데이터 포인트 쌍에 대한 일관성 모델의 출력의 차를 최소화하여 consistency distillation loss를 유도할 수 있다.

 

θ-는 θ의 EMA 모델

 

요약:

 

자세한 이론에 관심 없으면 여기까지만 알아도 됩니다.

---

다음으로 asymptotic analysis을 기반으로 일관성 증류에 대한 이론적 정당성 제공. 

뭣;

정리 1

f(⋅,⋅;Φ)는 경험적 PF ODE(score model)의 일관성 함수. ∆t는 그중 n의 간격이 가장 큰 경우.

f_θ가 lipschitz condition을 만족한다고 가정하면 모든 t, x, y에 대해 해당 식을 만족하는 L이 존재하며,

모든 n에 대해 t_n+1에서 호출된 ODE solver는 O(omitted, 임의의 오차항을 의미)로 uniformly bound 된 local error를 갖는다.

그리고 L = 0이면 해당 식을 얻는다.

 

 

증명

학습을 통해 일관성 증류 손실을 0으로 만들었다고 해보자.

 

λ(⋅)가 0이 아닐 경우:

 

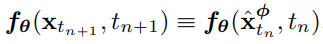
일관성 모델의 출력과 경험적 PF ODE의 일관성 함수의 출력 간의 error vector를 e로 표기:

 

PF ODE는 결정론적(일관적)이기 때문에 f(x_tn+1, t_n+1; Φ) = f(x_tn, t_n; Φ) 이고

다음과 같은 재귀 관계를 도출할 수 있다.

 

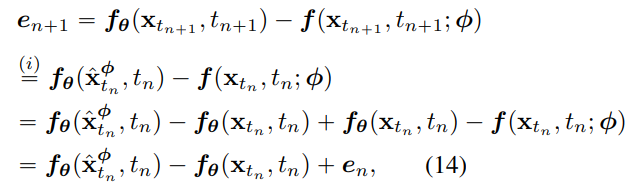
f_θ가 lipschitz constant L을 갖기 때문에

 

 

아무튼 그래서 이렇게 되는데

여기서도 할 말이 있는데 저렇게 오차항을 표기하는 것을 다른 ODE solver 논문에서도 봤다.

자주 쓰여서 암묵적으로 다들 알고 있는 표기인 건가?

설명도 당연한 듯이 '저런 형태의 local error'를 갖는다.' 라고만 되어있다.

 

일관성 모델의 경계 조건 때문에 e₁ = 0

 

아무튼 위의 공식들을 종합하면 아래와 같은 귀납을 수행할 수 있다.

 

최종적으로

 

솔직히 말하자면 이 정리가 도대체 어떤 깊은 의미가 있는 건지 잘 모르겠다. 해석학적으로 뭔가 있으려나.

 

 

 

Training Consistency Models in Isolation

Lemma 1.

p_t(x_t)가 p_data(x)에 가우스 분포를 컨볼루션 한 형태일 때,

(위에서 언급하지 않았지만 PF ODE를 소개할 때부터 이러한 노이즈 섭동을 사용하고 있었다.)

다음과 같은 score function을 추정할 수 있다.

 

즉, x와 x_t가 주어지면 몬테카를로 방법을 사용할 수 있다.

 

N → ∞ 일 때, Euler ODE solver의 추정값이 사전 훈련된 확산 모델을 대체하기에 충분하다는 것을 보여준다.

 

 

정리 2

d와 f_θ-는 bound 된 2차 도함수를 사용하여 연속적으로 두 번 미분 가능하고, λ(⋅)가 bound 되고, 기댓값이 < ∞이고, Euler ODE solver를 사용하고, 사전 훈련된 score model이 ground truth와 일치한다고 가정하면 다음과 같고

일관성 훈련 목표 L_CT는 다음과 같이 정의된다.

게다가,

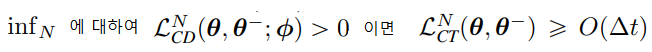
Lemma 1과 Theorem 2의 증명은 부록 A.3에...

 

CT loss는 score model Φ에 의존적이지 않고, 식 (9)에서 CT loss는 o(∆t) 보다 느리게 감소해 N → ∞, ∆t → 0 동안 식 (9)를 지배하게 된다.

 

추가로 성능 향상을 위해 N을 점진적으로 증가시킬 것을 제안한다.

아래 그래프를 보면

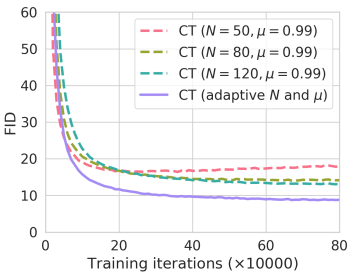
N이 작을 때는 분산이 적고 편향이 커 빨리 수렴하고, N이 클 때는 반대로 느리지만 품질이 더 좋다.

 

요약: 경험적 PF ODE(score model)가 하던 역할을 Euler ODE solver로 바꾸고 N을 점진적으로 증가시키는 전략을 도입하였다.

일관성 증류와 비교해 보자.

 

논문 부록 B에서 CD와 CT의 연속 시간으로의 확장에 대한 정리를 제공한다.

 

 

 

Experiments

이미지 품질이 최첨단 모델들과 견줄만한 수준은 아니지만 겨우 1 step 또는 2 step으로만 생성된 것을 생각하면 놀랍다.