DPM-solver에서 속도 개선, guided sampling에서도 작동되게 개선.

Abstract
Guided sampling을 위한 DPM-solver.
또한 임계값 방법과 DPM-solver++의 multi-step 변형 제안.
Introduction
DPM-solver에서는 유도(guided) 샘플링에 대해 제대로 조사하지 않았다. 유도 샘플링의 경우 단순한 1차 solver인 DDIM보다도 좋지 않았다고 한다.
데이터 예측 매개 변수화로 ODE를 해결하기 위한 solver를 도출하고, train-test 불일치 문제를 완화하기 위해 동적 임계값 방법을 채택한다. 또한, 불안정 해결을 위해 다단계 solver를 개발.

Background
Guided Sampling
Challenges of High-Order Solvers for Guided Sampling
고차 ODE solver의 유도 샘플 품질은 1차 ODE인 DDIM보다 나쁘다. 큰 지침 척도는 ODE solver의 수렴 범위에 영향을 미치며 고차 solver 일수록 더 예민하다.
또 다른 문제는 train-test 불일치이다. 데이터는 경계 구간 안에 있는데, 높은 지침 척도는 샘플을 경계 밖으로 떨어지게 한다.
Designing Training-Free Fast Samplers for Guided Sampling
표기법은 DPM-solver를 따름.
이전의 고차 solver는 노이즈 예측 모델 ε̃θ를 위해 설계되었지만, 본 논문에서는 데이터 예측 모델 xθ에 대한 ODE를 해결한다.

xθ는 그 자체로 몇 가지 이점이 있으며 경계를 유지하기 위한 임계값 방법을 적용할 수 있다.
Designing Solvers by Data Prediction Model
DPM-solver에서 정리한 xt의 해를

xθ의 change-of-variable form으로 나타내면 다음과 같다.

DPM-solver에서와 똑같이 테일러 전개 이용

또 똑같이 오차항O(h)를 생략하면 추정해야 하는 것은 n차 미분항 xθ(n) 뿐이다.
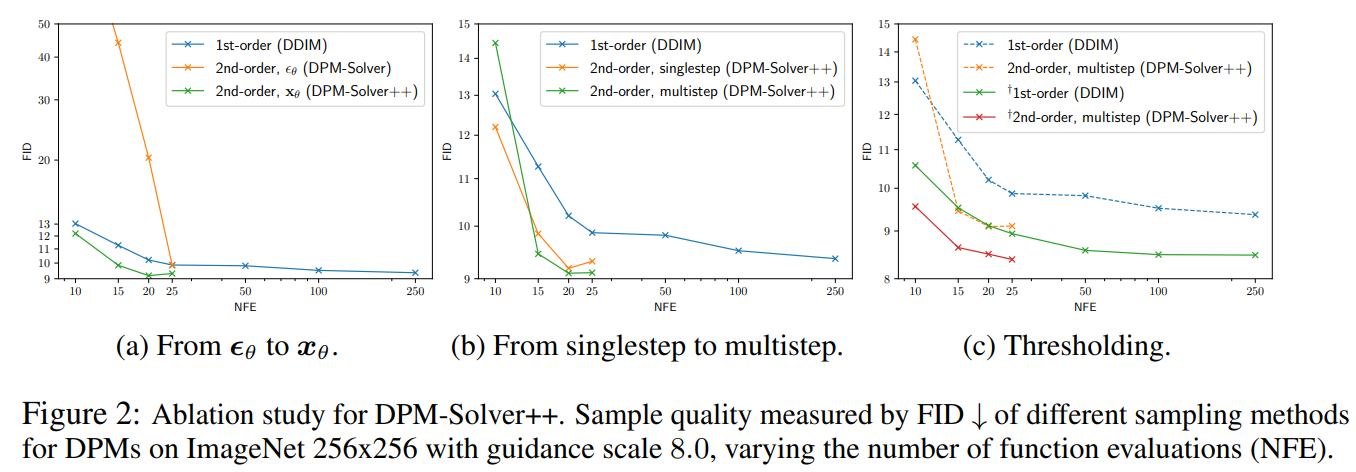
k=1 일 경우 solver는 DDIM과 동일,
k=2 일 경우 DPM-solver와 같이 중간 시간 단계 si를 도입하고, si와 ti-1의 함숫값을 결합하여 근사화하며 2M+1의 시간 단계가 필요하다.

From Singlestep to Multistep
위 알고리즘의 단일 단계 solver는 두 번의 function evaluation이 필요하고 중간 값 ui는 한 번 쓰이고 버려지기 때문에 비효율적이다. 따라서 이 섹션에서는 각 단계에서 이전 정보를 사용하는 solver를 제안한다.
중간 값이 아니라 x̃ti-1과 x̃ti-2를 결합하여 x̃ti를 계산한다.

다단계 방법은 단일 단계 방법보다 2배나 적은 시간 단계(=더 적은 function evaluation)가 요구되므로 오차항 O(h)도 더 작다.
Combining Thresholding with DPM-Solver++
임계값 방법은 데이터 경계 내에서 원래 모델 xθ를 요소별로 클리핑해 클리핑된 데이터 예측 모델 x̂θ를 정의하는 것이다.
DPM-solver++는 xθ를 위해 설계되었기 때문에 바로 결합할 수 있다.
Relationship with Other Fast Sampling Methods
DDIM도 일종의 1차 ODE-solver이며 DPM-solver++는 일종의 DDIM 고차 일반화이다.

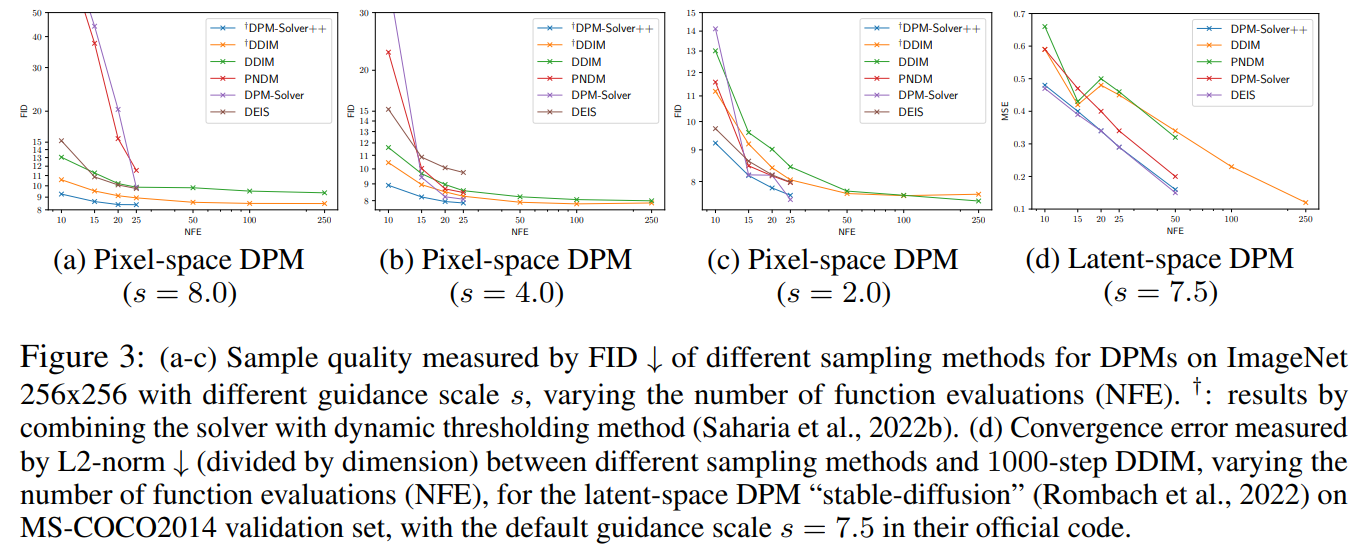
Experiments