ODE solver를 이용한 빠르고 고품질의 샘플링
테일러 전개로 DDIM보다 더 많은 시간 단계를 뛰어 넘음

Abstract
Diffusion probabilistic model(DPM)의 샘플링은 일반적으로 대규모 순차 단계가 필요하기 때문에 오래 걸린다. (SDE)
DPM의 샘플링은 확산 상미분 방정식(ODE)을 해결하는 것으로 대안적으로 볼 수 있다(DDIM). 본 논문에서는 확산 ODE 솔루션의 정확한 공식을 제안하고 모든 term을 블랙박스 ODE solver에 맡기는 대신 솔루션의 선형 부분을 분석적으로 계산한다.
아무튼 ODE를 위한 전용 solver인 DPM-solver를 제안한다. DPM-solver는 별도의 훈련 없이 20번 이하의 적은 단계로 고품질 샘플을 생성할 수 있게 한다.
Introduction
확산 ODE는 선형 함수와 비선형 함수로 구성된 semi-linear 구조를 가지고 있다. 이러한 구조를 활용하기 위해 선형 부분을 분석적으로 계산하여 확산 ODE 솔루션의 정확한 공식을 도출한다.
또한 변수 변화를 적용하여 솔루션을 신경망의 exponentially weighted integral로 단순화할 수 있다. 해당 적분을 근사화하여 DPM-solver를 제안한다.
구체적으로, DPM-solver의 1,2,3차 버전과 adaptive step size schedule을 제안.
DPM-solver는 연속 시간 및 이산 시간 DPM과 조건부 샘플링에도 모두 적용 가능. 매우 빠르게 고품질 샘플을 생성할 수 있다.
(NFE = number of function evaluations, SDE에서의 steps = ODE에서의 function evaluations와 비슷)

*들어가기에 앞서 본 논문의 수학 심화적인 부분은 제 이해력과 표현력의 한계로 그냥 기록용으로만 대충 씁니다. 진짜 수학적인 부분이 자세하게 궁금한 분들은 그냥 논문을 보세요... 사실 저도 잘 몰라요...
Diffusion Probabilistic Models
이 단원의 더 자세하고 이해하기 쉬운 설명(이것만 읽어도 됨.)
Forward Process and Diffusion SDEs
순방향

α(t), σ(t)는 미분 가능 함수.(노이즈 스케줄)
해당 논문에서 다음의 확률 미분 방정식(SDE)이 모든 t에 대해 식 2.1과 같은 동일한 transition distribution을 가지고 있음을 증명함.

역방향도 가능
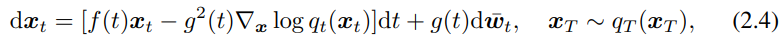
위 식에서 알 수 없는 것은 score 함수 ∇xlog qt(xt)인데, 이것은 신경망으로 추정함.
신경망의 피라미터 θ는 다음 식을 최소화함으로써 최적화됨.

이것은 일반적인 노이즈 예측 모델이다.
식 2.4의 score 함수를 모델로 대체한다.

전통적인 샘플링 방식은 식 2.5에 대한 1차 SDE solver로 볼 수 있다. 수많은 단계를 포함하므로 속도가 매우 느리다.
Diffusion (Probability Flow) ODEs
SDE에서 노이즈 항을 떼고 ODE로 변형.

모델로 대체.

ODE는 무작위성이 없기 때문에 더 큰 단계를 해결할 수 있지만 아직 느림.
Customized Fast Solvers for Diffusion ODEs
Simplified Formulation of Exact Solutions of Diffusion ODEs
수학 관심 없으면 핵심 통찰과 마지막 부분만 읽어도 됨.
본 연구의 핵심 통찰 첫 번째: time s > 0인 초기값 xs가 주어지면, 확산 ODE의 각 시간 t(< s)에서 솔루션 xt는 효율적으로 근사할 수 있는 매우 특별하고 정확한 공식으로 단순화될 수 있다.
식 2.7을 보면, ODE는 xt의 선형 함수와 신경망의 비선형 함수로 이루어진 semi-linear 상태이다. Semi-linear ODE의 경우 시간 t에서의 해는 variation of constants 공식에 의해 정확하게 공식화 될 수 있다.

블랙박스 ODE 솔버와 달리, 선형 부분은 이제 정확하게 계산되어 선형 항의 근사 오차가 제거된다.
핵심 통찰 두 번째 : 특수 변수를 도입함으로써 비선형 부분의 적분을 크게 단순화할 수 있다.
λt를 다음과 같이 정의하면 λt는 t에 대한 엄격한 감소 함수라고 할 수 있다.

그러면 식 2.3의 g(t)를 다음과 같이 쓸 수 있고

식 2.3의 f(t) = d log αt/dt 와 결합하면 식 3.1을 다시 쓸 수 있다.
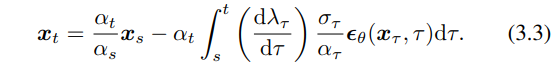
그리고 아무튼 여차저차 해서...

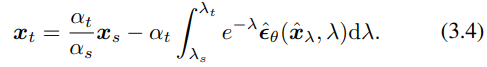
위 식의 비선형 부분을 지수 가중 적분이라고 명명한다.
위 식에 따르면, xs가 주어졌을 때 시간 t에서 솔루션을 근사하는 것은 ε̂θ의 지수 가중 적분을 λs에서 λt로 직접 근사하는 것과 동일하다.
High-Order Solvers for Diffusion ODEs
선요약 : ODE 관련 논문에서 알려진 지식과 k-1차 테일러 전개를 이용해 k차 DPM-solver-k를 도출할 수 있고 고차 solver일수록 더 많은 function evaluation이 필요하지만 수렴에 훨씬 적은 단계가 필요해 효율적이다.
시간 T에서의 초기값을 xT, M+1 단계 time step을 {ti}Mi=0, t0 = T, tM = 0, x̃t0 = xT로 정의.
M 단계 솔루션에서 각 단계에 대한 근사 오차를 줄여야 한다.
식 3.4에 따라, 해 xti-1 → ti는 다음과 같다.

아무튼 지수가중적분항을 근사해야 하고... 테일러 전개를 이용...

식 3.5를 다시 쓰면...

이러면 n차 총미분 ε̂θ(n)만 근사하면 되고, 이는 ODE 관련 논문에서 잘 알려진 문제라고 함...
오차항 O(h)를 버리고 논문에 따라 “stiff order conditions”으로 근사함으로써 확산 ODE에 대한 k차 ODE solver를 도출할 수 있다.
시연을 위해 k=1인 DPM-solver-1을 살펴보면 식 3.6은
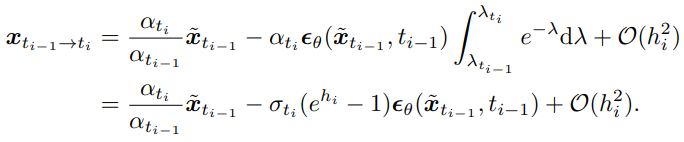
여기서 오차항 O(h)를 떨구면 xti-1 → ti의 근사치를 얻을 수 있고 이를 DPM-solver-1이라고 함.

k >= 2인 경우, 근사하려면 t와 s 사이의 추가 중간점이 필요하다. 자세한 것은 논문 부록 B 참조.

DPM-solver-k는 단계 당 k개의 function evaluation을 필요로 하지만 수렴하는 데 훨씬 적은 단계를 필요로 하기 때문에 더 효율적이다.
Step Size Schedule
Step size는 균일한 간격 or 적응형 단계 크기 알고리즘(논문 부록 C)을 사용하는데 number of function evaluations =<20인 경우 균일한 간격을, 나머지에서는 적응형 알고리즘 사용.
Sampling from Discrete-Time DPMs
이산 시간 확산 모델의 경우 N개의 정수 단계를 다음과 같이 나눔. (연속 시간 단계에서는 SNR을 시간 단계로 사용함.)
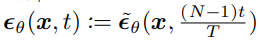
이러면 시간 단계가 정수가 아니게 되지만 smooth time embeddings(e.g., position embeddings) 때문인지 이상 없이 작동한다고 한다. 입력 시간이 정수가 아니게 됐으니 사실상 연속 시간 단계임.
Experiments




