Progressive Distillation for Fast Sampling of Diffusion Models

점진적 증류를 통해 샘플링 시간 줄임

 

Github

arXiv

 

Abstract

적은 샘플링 단계를 사용할 때 향상된 안정성을 제공하는 확산 모델의 새로운 매개변수화.

결정론적 확산 샘플러를 새로운 확산 모델로 추출하는 방법.

 

 

 

Introduction

사전 훈련된 확산 모델에 대한 N-step DDIM sampler의 동작을 샘플 품질의 저하가 거의 없는 N/2 단계의 새 모델로 증류하는 절차를 제시.

 

점진적 증류를 통해 샘플링 시간을 수십 배 줄이면서 샘플 품질을 유지함.

 

 

 

Background on Diffusion Models

(겁먹지 마세요. 이 부분은 잘 몰라도 됩니다.)

미분 가능한 log SNR

 

확산 모델의 순방향 과정

 

Denoising 모델을 통한 노이즈 제거

 

일반적인 Discrete time sampling

 

Probability flow ODE

 

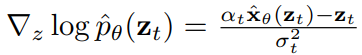
ODE를 풀기 위한 DDIM sampler의 업데이트 규칙

 

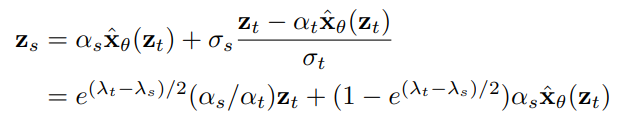
ODE의 수치 적분에 의해 도입된 오류는 적분 단계의 수가 무한히 커지면 0에 수렴함. 적분 단계와 품질의 trade-off 필요.

 

본 논문에서는 정확하지만 느린 ODE 적분기를 빠른 모델로 추출하는 방법을 제안함.

 

 

 

Progressive Distillation

교사 모델의 복사본으로 학생 모델을 초기화하고, 교사 모델의 DDIM sampling 2단계가 학생 모델의 1단계와 같도록 학습.

 

 

구체적으로, 학생 모델의 예측값인 x̃로 z_t''를 재구성하면

위 값이 교사 모델의 z_t''와 일치하도록 한다면 학생 모델의 예측값은 다음과 같아야 한다.

 

목표값 x̃(z_t)는 교사 모델과 시작점 z_t에 대해 완전히 결정론적이므로 예리한 예측을 할 수 있다.

 

또한 반복적으로 점진적 증류를 실행하고, 원래의 DDPM과 달리 T단계의 SNR이 0인 상태의 이산 시간에서부터 실행한다.

 

 

 

Diffusion Model Parameterization Training Loss

Denoising 모델을 매개변수화 하는 방법과 재구성 손실 가중치를 지정하는 방법에 대해 설명한다.

 

인 표준 프로세스에서 DDPM의 ε-prediction은 weighted x-prediction으로 볼 수 있다.

 

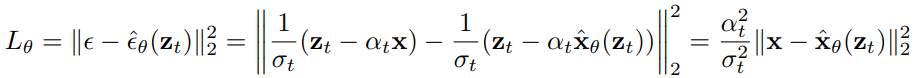
점진적 증류는 광범위한 SNR에서 평가되는데, α=0에 가까워질수록 예측의 작은 변화가 미치는 영향력이 증폭되고, 초기 샘플링에서 오류가 발생한다.

 

많은 sampling step을 수행할 때는 문제가 되지 않지만, 적은 step을 가지는 증류된 모델의 경우에는 ε-prediction과 x-prediction의 관계가 무너질 수 있다.

 

따라서 SNR의 변화에 민감하지 않은 매개변수화가 필요하다.

 

대안적인 매개변수화 방법 제시. 3가지 방법 모두 점진적 증류에 잘 맞았다고 한다.

• x를 직접 예측
• x와 ε을 같이 예측하고,  x와 ε을 결합하여 x̂ 정의
• v-prediction

SNR을 다음과 같이 표현하고

그러면

Velocity v를 다음과 같이 정의

그러면(증명부록)

 

 

각 값의 관계도

 

중요한 건 z_t와 velocity를 알면 z_s를 예측할 수 있고, v-prediction이 SNR에 민감하게 반응하지 않는다는 것이다.

 

매개변수화 방법 외에도 중요한 것은 재구성 손실의 가중치를 결정하는 것이다.

DDPM에서는 SNR이 0일 때 암시적으로 0의 가중치를 부여하므로 적합하지 않다.

 

α=0에 수렴해도 관계가 무너지지 않는 새로운 재구성 손실 제안: