Abstract
MCTS(Monte Carlo Tree Search)를 활용하여 인간 주석 데이터 없이 LLM의 수학 추론 프로세스 개선
[arXiv](2024/05/06 version v1)
Preliminary
수학 문제 해결을 강화 학습의 관점에서 바라본다.
먼저 문제 해결 과정을 T개의 추론 단계로 나누고 t 시점의 상태를 s, 다음 추론을 a라 할 때, 언어 모델은 정책의 역할을 한다.
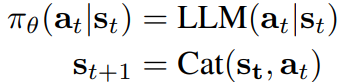
가치 함수 V를 통해 s에서 보상의 기댓값을 평가할 수 있다.
V는 일반적으로 N번의 시뮬레이션을 통해 보상을 집계하는 몬테카를로 평가를 사용하여 훈련된다.


Our Method
MC 평가보다 효율적인 Monte Carlo Tree Search (MCTS) 알고리즘을 통해 V를 훈련하는 방법을 제안.
MCTS 소개 섹션에서는 사전 훈련된 가치 함수 V와 LLM 정책 모델이 존재한다고 가정한다.
MCTS Evaluation

Selection
State-action value Q, upper-confidence bound 등을 고려하여 leaf node를 만날 때까지 트리를 검색한다.
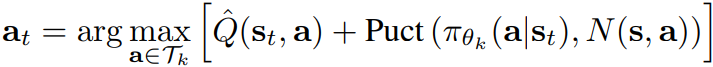
Expansion
LLM을 통해 후보 토큰을 샘플링한다.
Evaluation
V를 통해 각 후보를 평가한다.
원래는 시뮬레이션도 필요하다. 하지만 효율성을 위해 λ = 0으로 설정하고 가치 함수에 의존한다.
가치 함수는 후술 할 self-eval을 통해 업데이트할 수 있으므로 완벽하지 않아도 괜찮다.
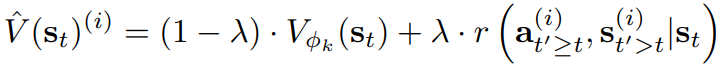
Backup
Q와 방문 횟수 N을 업데이트한다.
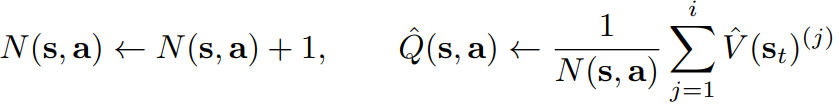
Self-Eval
위의 과정을 N번 반복하여 최종 트리 T를 얻은 후,
s에서 모든 a에 대한 기댓값의 평균이 V(s) 임을 이용하여

st에서의 기댓값을 근사할 수 있다.

또한 비종단 노드(최종 보상으로 연결되지 않는 노드)의 경우 다음과 같다고 가정하여 V를 구할 수 있다.


Iterative Training
먼저 그림의 오른쪽처럼 LLM에 V를 출력할 수 있는 sub-head를 추가한다.
정책과 가치 함수는 backbone을 공유한다.

정답과 오답을 각각 샘플링하고 nll loss를 통해 정책을, MCTS로 구한 Ṽ를 통해 가치 함수를 훈련한다.

업데이트된 정책과 가치 함수로 새로운 MCTS를 반복한다.
Inference
모델 배포를 위해 추론 시 MCTS를 beam search로 단순화한다.

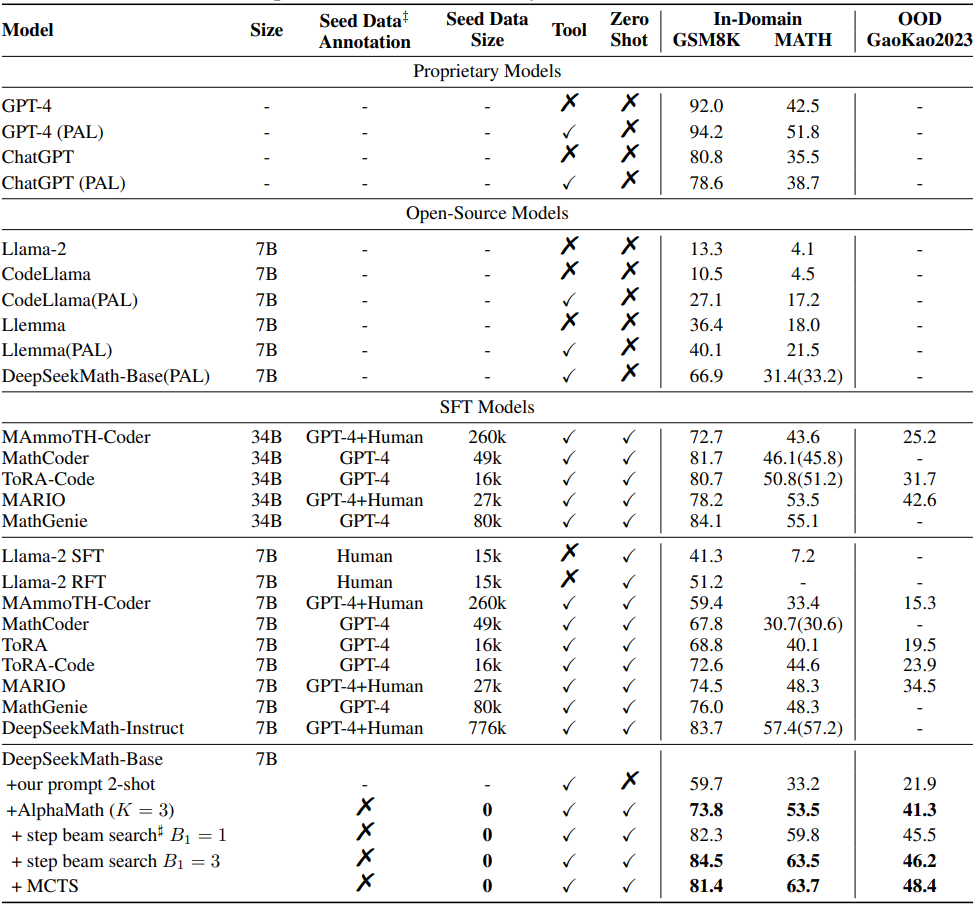
Experiments
Math LLM인 DeepSeekMath를 기반으로 한다.