LoRA: Low-Rank Adaptation of Large Language Models

사전 훈련 네트워크 가중치의 rank를 분해하여 효율적인 downstream 작업

 

Github

arXiv

 

 

Abstract

사전 훈련된 모델 가중치를 동결하고 transformer architecture의 각 계층에 훈련 가능한 rank decomposition matrix를 주입하여 다운스트림 작업에서 피라미터의 수를 크게 줄이는 Low-Rank Adaptation(LoRA) 제안.

 

 

 

Introduction

LoRA는 Measuring the Intrinsic Dimension of Objective Landscapes에서 영감을 받았다.

연구진은 모델 적응 중의 가중치 변화가 낮은 intrinsic rank를 갖고 있다고 가정하고 LoRA(Low-Rank Adaptation)를 제안했다.

 

LoRA는 위 그림과 같이 사전 훈련 가중치를 동결하고 대신 밀도 높은 계층에 대한 rank decomposition matrix를 최적화하여 매우 낮은 rank에서 간접적으로 훈련할 수 있다.

 

 

들어가기에 앞서 용어 및 규약 정리

모델의 입출력 차원 수 = d_model

사전 훈련된 가중치 행렬 = W or W₀

누적된 gradient = ∆W

rank = r

 

 

 

Problem Statement

언어 모델링을 중점으로 설명.

 

사전 훈련된 가중치 Φ₀에 대한 finetuning은 context-target 데이터 쌍 x, y에 대해 Φ₀ + ∆Φ로 업데이트 하는 것이다.

 

본 논문에서는 전체 가중치가 아닌 훨씬 작은 크기의 피라미터 집합으로 인코딩된 ∆Φ = ∆Φ(Θ)에서 Θ에 대한 최적화를 수행한다.

 

 

 

Method

Low-Rank Parametrized Update Matrices

네트워크를 instrinsic dimension에 투영한 이전 연구들과 달리 instrinsic rank를 갖는다고 가정하고 ∆W를 rank 분해 행렬곱으로 표현

 

다음과 같은 전진패스 산출.

W₀는 고정하고 A는 무작위 가우스, B는 0으로 초기화한다.

 

추론에 추가적인 비용이 거의 들지 않고 다른 작업으로 전환할 때는 AB를 뺀다음 다른 AB를 끼워넣기만 하면 되므로 편리하다.

 

모든 가중치 행렬에 LoRA를 적용할 수 있지만 효율성을 위해 attention projection matrix에만 적용한다.

 

다른 논문에서 가져온 예제인데 요런 느낌?

 

 

 

Understanding the Low-Rank Updates

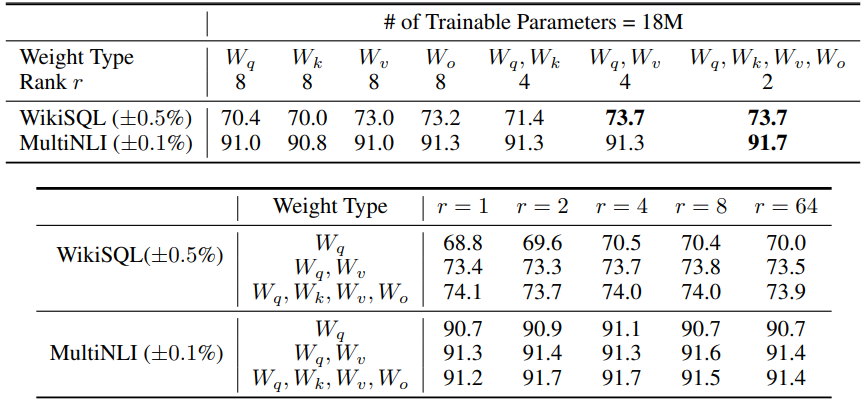
생각보다 엄청 낮은 rank를 사용하는데도 꽤 잘되는 모습?