[arXiv](2024/01/10 version v1)

Abstract
Score Distillation Sampling (SDS)를 심층적으로 분석하고 더 깨끗한 gradient를 제공하는 Score Distillation Sampling with Learned Manifold Corrective (LMC-SDS) 제안
Analysis
확산 손실:
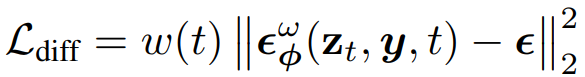


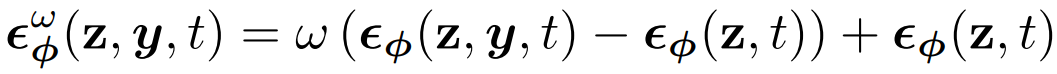
SDS를 다음과 같이 다시 쓸 수 있다.

w가 높으면 지나치게 채도가 높은 이미지와 아티팩트를 생성하고, 낮으면 지나치게 흐릿한 이미지를 생성한다.

이를 분석하기 위해 SDS rendering function g()가 ID인, 즉 z = θ인 경우에 각 score를 시각화하였다.

Lcond는 항상 prompt를 지키기 위해 과도하게 노력하여 과도한 색상이나 아티팩트를 가진 manifold에서 벗어난 gradient를 생성하고, Lproj는 이에서 기인하는 고주파 디테일을 제거하려고 하여 흐릿한 이미지를 생성하는 것이었다.
Method
한 가지 제안은 예측된 노이즈 대신 예측된 이미지 ẑt = zϕ(z, t)와 렌더링 된 이미지 z를 비교하는 것이다.

하지만 예측된 이미지는 z의 완벽한 복제가 아니며 z가 natural image manifold에 있는 경우에도 t가 클수록 더 그렇다.

따라서 denoising model의 동작을 natural image manifold로 투영(z → z̃)하는 p, denoising error b로 구분한다.
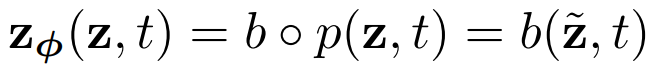
b는 수정할 수 없기 때문에(애초에 이 모든 짓을 하기 위한 목적이 증류이므로) 우리는 p에만 관심이 있으며, b를 근사한 b̂을 ẑt와 비교하기 전에 z에 적용한다.

(SDS와 마찬가지로 jacobian term을 생략하고 weighting term 또한 생략했을 때 경험적으로 품질이 좋아짐.)

b̂을 b̂ψ(z, t)로 학습 가능한 피라미터화하고 (z, ẑt, t)에 대해 다음과 같이 훈련한다.

원본 b의 복잡성 때문에 b̂ψ는 과소 적합될 것으로 예상되며 이미지를 '흐리게' 하는 방법을 배운다. 또한 manifold로부터 정보를 얻지 않기 때문에 non-manifold 이미지에 대해서도 보정을 수행할 수 있다.
하지만 이대로 적용하면 이미지 통계에서 편향을 유발하여 과도하게 대조적인 이미지를 생성했기 때문에 정규화된 공간에서 손실을 계산하여 통계와 무관하게 만든다.
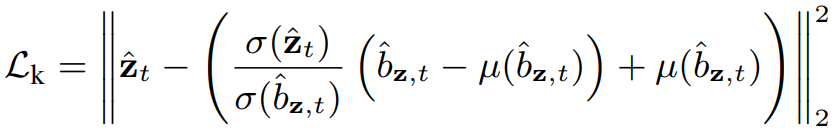
이러면 Llmc를 계산할 때도 정규화를 적용해야 한다.
Increasing Sample Diversity
연구진은 SDS에서 고정된 ϵ을 사용하는 것이 다양성 저하의 원인이라고 가정하고 Lcond에서는 고정된 ϵ을, Llmc에서는 ϵ을 계속 샘플링하였을 때 다양성이 향상되었다고 한다.
Implementation Details
b̂ψ의 architecture는 U-Net이다.
Experiments








