[Github]
[arXiv](Current version v1)
Abstract
MoE를 ViT에 적용하여 절반의 계산 비용으로 동일한 성능을 내는 V-MoE 제안
The Vision Mixture of Experts
Conditional Computation with MoEs
MoE는 라우팅 함수 g()를 통해 입력을 각 전문가 ei(x)에 할당한다.

g(x)가 희소한 경우 계산은 super-linear 하다.
MoEs for Vision
MLP layer에는 2개의 feedforward와 non-linearity가 있다.

MLP layer 중 일부를 MoE layer로 대체한다.
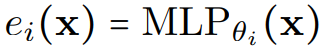

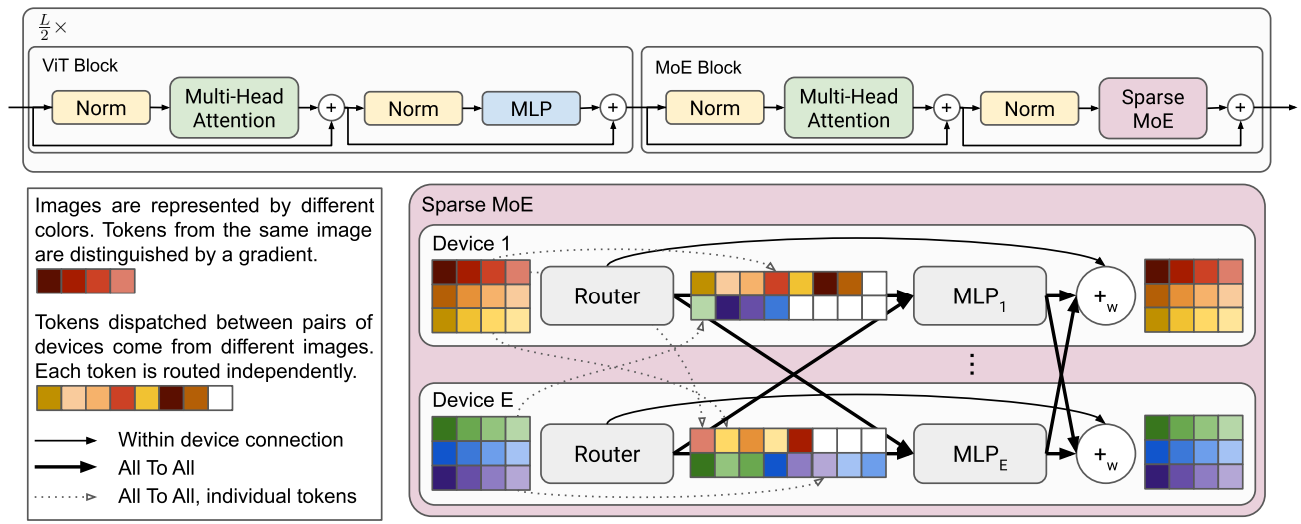
위 그림이 좀 헷갈릴 수 있는데, 계산 효율성을 위해 배치 이미지들을 각 분산 장치에 입력하고, MoE layer에서 토큰의 출신 이미지와 상관없이 같은 전문가에 할당된 토큰끼리 모아서 연산 후 다시 같은 이미지 출신끼리 묶는다.
Routing
각 토큰은 장치에 분산된 각 k개의 전문가에게 할당된다.
k = 1 or 2

MoE와의 차이점은 top-k보다 softmax를 먼저 적용한다는 것이다. 노이즈의 표준 편차 = 1/E

Expert’s Buffer Capacity
소수의 전문가만이 선호되는 현상을 막기 위해 각 전문가가 처리할 수 있는 토큰 수를 제한한다.
버퍼 용량보다 작은 토큰이 할당되면 0으로 채우고, 많은 토큰이 할당되면 최대 용량까지만 처리되지만 잔차 연결로 보존되기 때문에 해당 토큰이 '분실'되지는 않는다.
용량 비율 C를 도입한다. 지정된 C의 값에 따라 버퍼 용량보다 더 적거나 많은 수의 토큰을 처리할 수 있는데, 이는 매우 다른 분포에서 fine-tuning 시에 사용한다.
아래에는 load balancing을 위한 손실을 설명한다.
Importance Loss
입력 배치 X와 g()의 가중치 W, 전문가 i에 대해 라우팅 출력의 softmax 합의 변동 계수:

MoE의 변동 계수 손실과 다른 점은 선택받지 못한 라우팅 가중치도 포함한다는 것이다.
Load Loss
한 전문가에 할당된 토큰들 중 k번째 최대 score를 임계값으로 지정하고

노이즈를 제거한 후 리샘플링한 노이즈를 추가했을 때 임계값을 넘을 확률
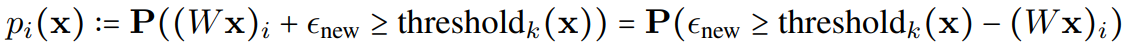
의 변동 계수:

Final Auxiliary Loss
그냥 평균
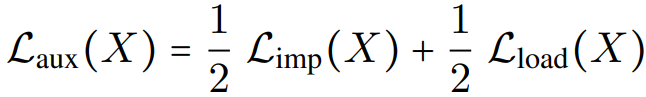
The overall loss
λ = 0.01로 큰 영향을 끼치지 않는다.

Skipping Tokens with Batch Prioritized Routing
모든 토큰이 똑같이 중요한 것은 아니며, 배경 패치와 같이 유용하지 않은 토큰을 폐기하고 작은 버퍼 용량을 사용할 수 있는 라우팅 알고리즘 제안.
Batch Prioritized Routing
배치에 속한 모든 토큰들을 전문가 i에 대한 가중치 내림차순으로 정렬하고 할당한다.
할당 시에 라우팅 가중치를 재사용하고, 배치 내의 모든 토큰이 경쟁하므로 어떤 이미지는 적은 컴퓨팅을 받을 수 있다.





