Zero-Shot Image Restoration Using Denoising Diffusion Null-Space Model

사전 훈련된 확산 모델을 이용한 zero-shot 이미지 복원 모델

 

https://paperswithcode.com/paper/zero-shot-image-restoration-using-denoising

Papers with Code - Zero-Shot Image Restoration Using Denoising Diffusion Null-Space Model

 

 

 

Abstract

추가 교육이나 네트워크 수정 없이 생성 prior로 사전 교육된 확산 모델만 있으면 되는 제로샷 이미지 복원 모델 Denoising Diffusion Null-Space Model (DDNM)을 제안. 이는 역확산 과정에서 null-space 내용만을 정제하는 것으로 다양한 작업 가능.

 

또한 강화 버전인 DDNM+도 있음.

 

 

 

Introduction

이미지 복원(IR)은 저하된 이미지 y (=Ax + n)에서 x̂을 생성하는 것이 목표.

 

일반적인 솔루션 :

첫째 항으로 데이터 최적화, 둘째 항은 자연스러운 이미지 분포에 대한 사전 지식으로 정규화를 담당한다.

 

DNN을 이용한 방법 :

위 방법들은 본질적으로 y에서 x로의 매핑 학습을 장려하기 때문에(직접 최적화) 다른 도메인에서 일반화 능력이 떨어짐.

 

사전 훈련 모델 g의 잠재 코드 w를 이용한 개선된 방법 :

---

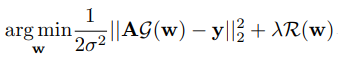
Range-Null space 분해에 대한 논문인데 수치해석 쪽은 자세히는 잘 몰?루 (어차피 밑에서 설명함)

어쨌든 적절한 null-space 콘텐츠를 찾는 것이 중요하고 확산 모델이 이상적인 null-space 콘텐츠를 산출할 수 있다고 한다.

---

DDNM은 최적화 또는 네트워크의 수정없이 역확산 과정에서 null-space 콘텐츠의 정제 만으로 현실적이고 일관성 있는 결과를 산출할 수 있다고 한다. 또한 super-resolution, colorization, compressed sensing, inpainting, deblurring 등 다양한 작업에서 최첨단 성능을 보여줌.

 

본 논문의 기여 

• 사전 훈련된 모델의 역확산 과정에서 null-space만 정제하여 제로샷 선형 IR 문제를 해결함.
• 복잡한 IR 문제 해결을 위한 time-travel trick 제시.
• 다양한 실험

 

 

 

 

Background

확산 모델 설명은 생략.

 

Range-Null Space Decomposition

선형 변환 행렬 A가 있을 때, 의사 역행렬 A+를 통해 샘플 x를 

(A⁺A는 x를 A의 range=column space로 투영시킨다, 참조)

A의 range space에 있는 부분(첫째 항), A의 null space에 있는 부분으로 분해할 수 있다.

 

x에 A를 적용하면 앞 항은 그대로 Ax가 되고(모든 성분이 행렬 A의 range space에 있기 때문에) 뒷 항은 0이 된다(모든 성분이 null space에 있기 때문에).

 

 

 

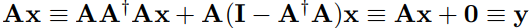
Method

Denoising Diffusion Null-Space Model

노이즈 없는 IR부터 시작.

 

y에서 다음 두 제약 조건을 준수하는 이미지 x̂을 생성하는 것을 목표로 함. (q(x) = ground truth의 분포)

---

일관성 제약과 range-null space 분해에 의해 목표인 x̂을 다음과 같이 정의할 수 있다.

x̄가 무엇이든 일관성에는 전혀 영향이 없기 때문에, 우리의 목표는 realness를 위한 적절한 x̄를 찾는 것이다.

 

Range space와 조화를 이루는 null space를 생성하기 위해 확산 모델을 이용한다.

---

 

x_t에서 깨끗한 이미지 x_0ㅣt를 얻는다. (사전 훈련 확산 모델로, 원래 DDPM과 같음.)

 

얻은 것을 null space 정보로 사용하고 range space는 고정하여 추정치 산출 (그림 참조)

이러한 방법으로 null space만 역확산 과정에 참여시킨다.

---

x_t-1은 말하자면 x̂_0ㅣt의 노이즈 추가 버전이며, 추가되는 노이즈는 계속해서 range-null space 간의 불일치를 지운다.

최종 결과는 모든 역확산 과정에서 일관성을 준수한 x₀ ~ q(x).

 

지금까지의 방법을 Denoising Diffusion Null-Space Model (DDNM) 이라고 함.

 

Examples of constructiong A and A⁺

Inpainting, colorizing, super-resolution 작업에서 A+를 간단히 설정하는 방법에 대해 알려주는 파트이다. 너무 지엽적이므로 pass.

 

DDNM+

DDNM은 특정 사례나 노이즈가 많은 상황에서 좋지 않기 때문에 강화 버전 제안.

 

노이즈가 많은 IR을 지원하기 위한 range-space 보정

노이즈가 많은 IR 문제를 y = Ax + n(랜덤 노이즈)으로 정의하면

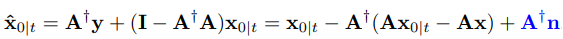
A⁺n은 추가적인 노이즈이며, 두 번째 항은 range-space를 건드리게 된다(A⁺A).

---

x̂_0ㅣt는 x_t-1의 평균을 구하는 데 사용되기 때문에 노이즈를 추가할 수 없다.

문제 해결을 위해 수정된 DDNM : (A⁺n을 떼고, 스케일링 계수(행렬) 추가)

Σ는 range-space를 건드는 부분을 스케일링, Φ는 추가될 노이즈를 스케일링한다.

 

두 계수는 두 가지 원칙에 의해 선택된다.

• Φ : 사전 훈련 모델이 t-1 단계에서 예측해야 할 노이즈의 분산(1 − ᾱ_t)을 준수
• Σ : Range-space의 보존을 위해 가능한 I에 가까워야 함

---

(이 부분은 몰라도 됨...)

위에 언급한 A+를 간단히 구할 수 있는 세  가지 IR 작업에 대해서는 다음과 같이 치환할 수 있고

 

원칙 1에 의해 :

원칙 2에 의해 :

 

다른 작업에 대해서는 특이값 분해로 구해야 함...

 

Non-Gaussian noise는 Gaussian noise로 근사해서 똑같이 하면 됨.

---

더 나은 복원을 위한 Time-Travel

SR with large-scale average pooling downsampler, low sampling ratio compressed sensing(CS), inpainting with a large mask 작업 등 range-space가 너무 국소적인 경우 낮은 realness가 관찰되었다.

 

확산 모델의 학습은 사후 분포 p(x_t−1|x_t, x₀)의 추정에 의존한다. 

DDNM에서 t 시점의 x₀ 추정치로 x̂_0ㅣt를 사용하는데, 이때 range-space가 너무 국소적이면 부조화스러운 null-space를 갖게 된다.

---

Time-travel은 명칭은 다르지만 최근 다른 논문들에서도 꽤 보이는 방법으로, t 시점에서 순방향 확산(q(x_t+l|x_t))으로 다시 t+l 시점으로 되돌아간 다음, 다시 DDNM을 진행하는 전략이다.

 

 

 

 

Experiments

Papers With Code에 들어가 보면 12월 7일 현재 꽤 많은 IR 작업들에서 SOTA거나 순위권인 성능을 보여준다.