Cold Diffusion : Inverting Arbitrary Image Transforms Without Noise

노이즈 이외의 다른 이미지 저하 방법을 위한 새로운 샘플링 알고리즘

 

Arxiv

Github

 

 

 

Abstract

연구진은 확산 모델의 생성적 동작이 이미지 저하의 선택에 크게 의존하지 않는다는 것을 관찰했으며 완전히 결정적인 저하(blur, masking 등)를 사용하는 경우에도 규칙을 쉽게 일반화하여 생성 모델을 만들 수 있다. 이러한 완전 결정론적 모델의 성공은 gradient Langevin dynamics 또는 변분 추론의 노이즈에 의존하는 확산 모델에 대한 의문을 제기하고 일반화된 확산 모델의 길을 열어준다.

 

 

 

Introduction

본 논문에서는 확산 모델이 실제로 작동하기 위해 가우스 잡음과 같은 랜덤성의 필요를 조사하고 확산 모델이 생겨난 이론적 프레임워크의 범위 밖에 있는 일반화된 확산 모델을 고려한다.

 

랜덤성이 필요하지 않은 cold-diffusion(낮은 랜덤성)의 존재는 확산 모델에 대한 이론적 이해의 한계에 대한 질문을 제기한다.

 

 

 

Generalized Diffusion

Model components and training

주어진 이미지 x₀에 대해 t만큼 저하 작업 D를 적용한 것을 x_t = D(x₀, t)라고 하고 다음을 만족함.

 

또한 D의 반대 연산을 수행하는 R

 

확산 모델의 목적(이하 신경망 θ 생략)

 

Sampling from the model

작은 t의 경우 R을 한 번만 적용하여 한 번에 복원된 이미지를 얻을 수 있지만, R은 L1 손실로 훈련되기 때문에 큰 t에서 흐릿한 결과가 생성된다.

 

DDPM에서는 역연산 과정에서 노이즈를 반복적으로 다시 추가함.

 

알고리즘 1이 노이즈 기반 확산에서 잘 작동하지만 매끄럽고 미분 가능한 저하를 갖는 저온 확산의 경우에는 좋지 않다는 것을 발견했고 저온 확산을 위한 새로운 알고리즘을 제안한다.

 

Properties of Algorithm 2

저온 확산에서 알고리즘 2는 완벽하지 않은 복원 연산 R에 관대하다. 이유를 알아보기 위해 D(x, s) ≈ x + s · e 형식의 선형 저하 함수가 있는 모델 문제를 고려한다.

 

귀납법을 통해 알고리즘 2가 R의 선택에 관계 없이 모든 s에 대해 x_s = D(x₀,s)를 생성한다는 것을 알 수 있다. 즉, R이 어떤 선택을 하든지 간에 R이 D의 완벽한 반전일 때와 동일하게 작동한다.

 

반면에 알고리즘 1은 R이 완벽하지 않을 때 고정적인 x₀를 생성할 수 없다.

 

윗줄 : 알고리즘 1은 저온 확산에 대해 안정적으로 작동하지 않는다.

 

 

 

Generalized Diffusions with Various Transformations

서로 다른 저하에 대한 이미지 생성 수행.

 

Deblurring

Gaussian blur 연산에 대한 확산.

(Direct = R(D(x₀,T)), Alg. = 알고리즘 2)

 

Inpainting

2D Gaussian curve 마스크를 이용해 픽셀들을 점진적으로 회색으로 만드는 저하.

 

Super-Resolution

 

Snowification

 

 

 

Cold Generation

Generation using deterministic noise degradation

고정된 노이즈로 "결정적" 샘플링을 하는 두 가지 방법 연구.

 

우선 고정된 노이즈 z와 데이터 포인트 x 사이의 결정론적 보간을 사용할 수 있다.

 

또는 다음 공식을 통해 t 단계에서 사용할 노이즈 z를 결정론적으로 계산할 수 있다. 이 방법은 DDIM과 유사함.

 

두 방법 비교

 

Image generation using blur

Blur로 완전히 저하된 이미지 x_T는 단일 색상으로, 샘플링하기 좋은 폐쇄형 분포를 가지고 있지 않다. 대신에 RGB 채널 평균으로 3-vector를 얻고 이에 대한 분포는 가우시안 혼합 모델로 표현 가능하다.

 

샘플링된 이미지는 낮은 주파수를 가지는데 픽셀 간의 대칭을 깨기 위해 x_T에 소량의 가우스 노이즈를 추가하면 생성 품질이 크게 향상된다.

 

Generation using other transformations

이 섹션에서는 blur에서의 생성을 다른 변환에까지 확장한다.

 

가우스 마스크 변환(위 섹션의 inpainting)의 완전한 저하는 모든 픽셀을 검게 하는 것이지만 생성 다양성을 위해 마스킹된 부분은 단일 색상으로 대체한다.

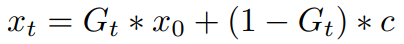
초해상도의 경우 최종 저하는 2x2의 1차원 벡터이며 이 분포에서 모델링 됨.

 

거의 모든 변환을 역전시킬 수 있다.