R1 gradient penalty in Which Training Methods for GANs do actually Converge?
GAN의 적대적 손실 함수:
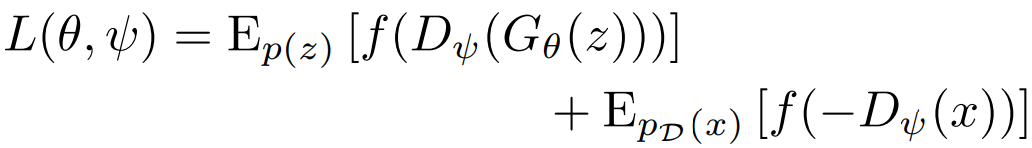
손실을 G는 최소화, D는 최대화하는 것이 목적이다.
GAN에서 Generator와 Discriminator의 고유한 내쉬 균형은 G의 생성 분포가 실제 데이터 분포와 같고 D가 항상 0을 내놓을 때이다. (D가 1/2을 출력할 경우는 고유하지 않음. 고유한가 아닌가는 중요하지 않지만.)
하지만 내쉬 균형점 근처에서 훈련이 불안정해진다.
왜? why?
생성 분포 G(z)와 데이터 분포 P가 떨어져 있는 경우에는 잘 구별한다.
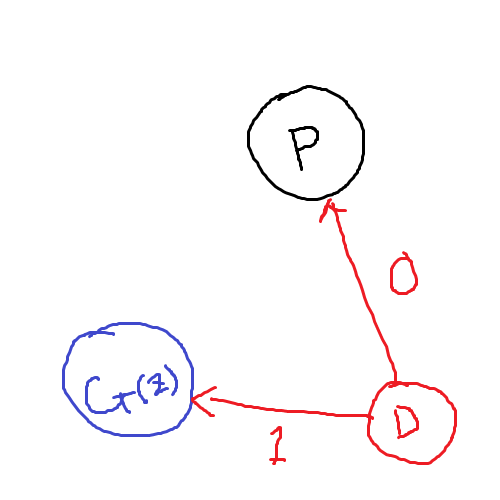
하지만 G의 성능이 엄청 좋아서 데이터 분포와 (거의)같은 분포를 생성할 경우에는?
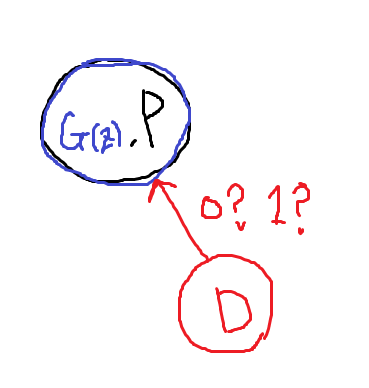
똑같은 분포에서 나온 데이터를 보고 둘로 나누어야 하므로 의미 없는 gradient가 발생하게 된다.
실제로 훈련이 수렴하지 못하고 타원 궤적이 그려진다.
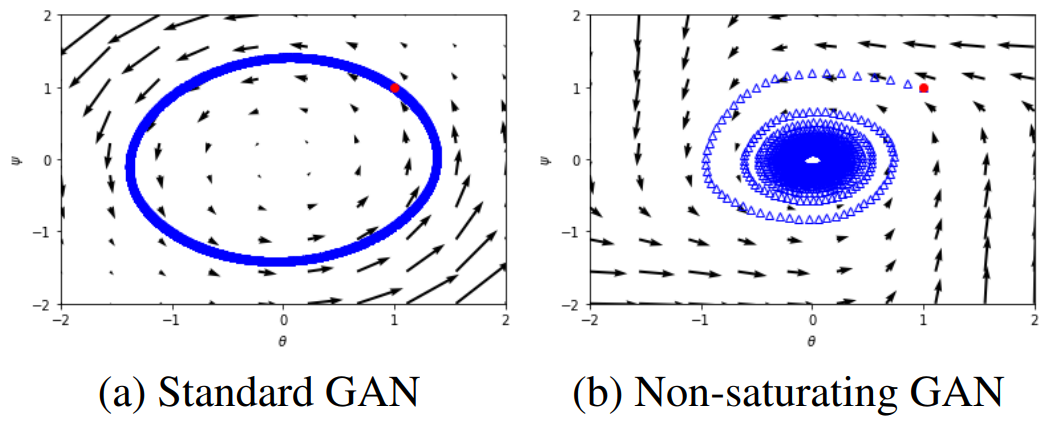
R1 gradient penalty는 간단하다.
실제 데이터 분포에 대해 생성된 0이 아닌 gradient에 penalty를 부여하는 것이다.
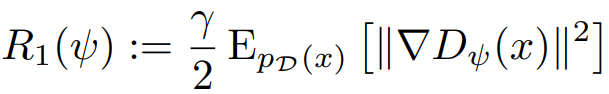
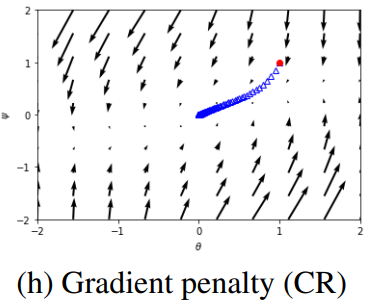
실제 데이터에 대한 D의 gradient가 점점 줄어들면서 수렴하게 된다.
직관적으로 설명하면 G(z)를 P라고 잘못 분류할지언정, P를 보고 P가 아니라고는 하지 말라는 거다.
Penalty로 인해 D가 0을 주는 범위가 고정되어 G도 편안하게 수렴 가능.
'논문 리뷰 > Concept' 카테고리의 다른 글
| Rotary Position Embedding (RoPE) (0) | 2024.03.04 |
|---|---|
| Constitutional DPO (0) | 2024.02.05 |
| Self-Conditioning (1) | 2023.12.17 |
| Score Distillation Sampling (1) | 2023.11.30 |



